
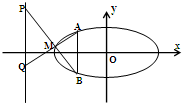
 已知椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{3}}}{2}$,直线l:x-y+1=0经过C的上顶点.又,直线x=-1与C相较于A、B两点,M是C上异于A、B的任意一点,直线AM、BM分别交直线x=-4于两点P、Q.
已知椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{3}}}{2}$,直线l:x-y+1=0经过C的上顶点.又,直线x=-1与C相较于A、B两点,M是C上异于A、B的任意一点,直线AM、BM分别交直线x=-4于两点P、Q.分析 (Ⅰ)判断椭圆焦点在x轴且b=1,利用a2-c2=1,$\frac{c}{a}=\frac{{\sqrt{3}}}{2}$,求解a,即可得到椭圆方程.
(Ⅱ)求出$\overrightarrow{OP}$•$\overrightarrow{OQ}$的表达式.设A(-1,t),B(-1,-t),将x=-1代入椭圆方程,求出AB坐标,设M(x0,y0),代入椭圆方程,求出AM方程,然后求解Q纵坐标,P的纵坐标,$\overrightarrow{OP}$•$\overrightarrow{OQ}$的表达式求出定值.
解答 解:(Ⅰ)依题意,椭圆焦点在x轴且b=1…1’,
即a2-c2=1,而$\frac{c}{a}=\frac{{\sqrt{3}}}{2}$…3’,
∴a=2…4’,
从而椭圆方程为$\frac{x^2}{4}+{y^2}=1$…5’.
(Ⅱ)∵$\overrightarrow{OP}=(-4,{y_P})$,$\overrightarrow{OQ}=(-4,{y_Q})$,
∴$\overrightarrow{OP}•\overrightarrow{OQ}=16+{y_P}•{y_Q}$…6’.
设A(-1,t),B(-1,-t),将x=-1代入C的方程,
得${t^2}=\frac{3}{4}$,∴A(-1,$\frac{{\sqrt{3}}}{2}$),B(-1,-$\frac{{\sqrt{3}}}{2}$)…7’,
又设M(x0,y0),代入C的方程,得$\frac{x_0^2}{4}+y_0^2=1$…8’,
AM:$y-t=\frac{{{y_0}-t}}{{{x_0}+1}}(x+1)$,令x=-4,
得${y_Q}=t-3•\frac{{{y_0}-t}}{{{x_0}+1}}=\frac{{-3{y_0}+({x_0}+4)t}}{{{x_0}+1}}$…9’,
同理,${y_P}=\frac{{-3{y_0}-({x_0}+4)t}}{{{x_0}+1}}$…10’,
∴${y_P}•{y_Q}=\frac{{{{(-3{y_0})}^2}-{{({x_0}+4)}^2}{t^2}}}{{{{({x_0}+1)}^2}}}$
=$\frac{{9(1-\frac{1}{4}{x_0}^2)-({x_0}^2+8{x_0}+16)•\frac{3}{4}}}{{{{({x_0}+1)}^2}}}$
=$\frac{{-3{x_0}^2-6{x_0}-3}}{{{{({x_0}+1)}^2}}}=-3$…11’,
得$\overrightarrow{OP}•\overrightarrow{OQ}=13$…12’.
注:若通过M与C的左端点重合的特殊情况得出$\overrightarrow{OP}•\overrightarrow{OQ}=13$,后无一般性证明,可打分至9’.
点评 本题考查直线与体育的位置关系的综合应用,向量与圆锥曲线综合,考查转化思想以及计算能力.


科目:高中数学 来源: 题型:解答题
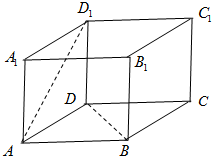 如图,已知直四棱柱ABCD-A1B1C1D1,DD1⊥底面ABCD,底面ABCD为平行四边形,∠DAB=45°,且AD,AB,AA1三条棱的长组成公比为$\sqrt{2}$的等比数列,
如图,已知直四棱柱ABCD-A1B1C1D1,DD1⊥底面ABCD,底面ABCD为平行四边形,∠DAB=45°,且AD,AB,AA1三条棱的长组成公比为$\sqrt{2}$的等比数列,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届甘肃兰州一中高三9月月考数学(文)试卷(解析版) 题型:选择题
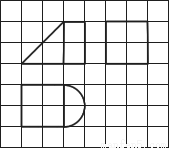
如图,网格纸上小正方形的边长为 ,粗实线画出的是某几何体的三视图,则该几何体的的体积为( )
,粗实线画出的是某几何体的三视图,则该几何体的的体积为( )
 B.
B. C.
C.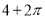 D.
D.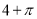
查看答案和解析>>
科目:高中数学 来源:2017届甘肃会宁县一中高三上学期9月月考数学(文)试卷(解析版) 题型:解答题
在扶贫活动中,为了尽快脱贫(无债务)致富,企业甲将经营状况良好的某种消费品专卖店以5.8万元的优惠价格转让给了尚有5万元无息贷款没有偿还的小型企业乙,并约定从该店经营的利润中,首先保证企业乙的全体职工每月最低生活费的开支3 600元后,逐步偿还转让费(不计息).在甲提供的资料中:①这种消费品的进价为每件14元;②该店月销量Q(百件)与销售价格P(元)的关系如图所示;③每月需各种开支2 000元.

(1)当商品的价格为每件多少元时,月利润扣除职工最低生活费的余额最大?并求最大余额;
(2)企业乙只依靠该店,最早可望在几年后脱贫?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com