
分析 (Ⅰ)当a=2时:f(x)≥-4即:|x+2|-|2x-2|≥-4.通过x≤-2,-2<x≤1,1<x,去掉绝对值符号,然后求解不等式即可.
(Ⅱ)通过a>-4,a=-4,a<-4,化简函数的解析式,利用f(x)≤4,对x∈R成立,通过函数的最值,转化不等式,求解a的取值范围.
解答 解:(Ⅰ)当a=2时:f(x)≥-4即:|x+2|-|2x-2|≥-4.
等价于$\left\{\begin{array}{l}{x≤-2}\\{-2-x+2x-2≥-4}\end{array}\right.$或$\left\{\begin{array}{l}{-2<x≤1}\\{x+2+2x-2≥-4}\end{array}\right.$或$\left\{\begin{array}{l}{x>1}\\{x+2-2x+2≥-4}\end{array}\right.$…(3分)
解得:x∈∅或x∈[$-\frac{4}{3}$,1]或x∈(1,8]
故不等式的解集为$[{-\frac{4}{3}}\right.,\left.8]$…(5分)
(Ⅱ)当$-2<\frac{a}{2}$即:a>-4时:$f(x)=\left\{\begin{array}{l}x-a-2,x<-2\\ 3x+2-a,-2≤x≤\frac{a}{2}\\-x+a+2,x>\frac{a}{2}\end{array}\right.$,
∴f(x)在$({\frac{a}{2},+∞})$上递增,在$({\frac{a}{2},+∞})$上递减
依题意:$f({\frac{a}{2}})=|{\frac{a}{2}+2}|≤4$解得:-4<a≤4…(7分)
当$-2=\frac{a}{2}$,即a=-4时:f(x)=-|x+2|≤4对x∈R恒成立 …(8分)
当$-2>\frac{a}{2}$,即$f(x)=\left\{{\begin{array}{l}{x-a-2,x<\frac{a}{2}}\\{-3x+a-2,\frac{a}{2}≤x≤-2}\\{-x+a+2,x>-2}\end{array}}\right.$
∴f(x)在$({-∞,\frac{a}{2}})$上递增,在$({\frac{a}{2},+∞})$上递减
依题意:$f({\frac{a}{2}})=|{\frac{a}{2}+2}|≤4$,解得:-12≤a<-4
综上所求:a的取值范围为[-12,4]. …(10分)
点评 本题考查函数恒成立,绝对值不等式的解法,函数的单调性以及函数的最值的综合应用,考查分类讨论思想以及转化思想的应用,考查计算能力.


科目:高中数学 来源: 题型:解答题
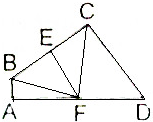 如图所示,四边形ABCD中,AB=1,AD=7,BC=CD=5,∠BAD=∠BCD=90°.
如图所示,四边形ABCD中,AB=1,AD=7,BC=CD=5,∠BAD=∠BCD=90°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
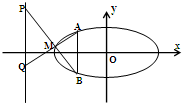 已知椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{3}}}{2}$,直线l:x-y+1=0经过C的上顶点.又,直线x=-1与C相较于A、B两点,M是C上异于A、B的任意一点,直线AM、BM分别交直线x=-4于两点P、Q.
已知椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{3}}}{2}$,直线l:x-y+1=0经过C的上顶点.又,直线x=-1与C相较于A、B两点,M是C上异于A、B的任意一点,直线AM、BM分别交直线x=-4于两点P、Q.查看答案和解析>>
科目:高中数学 来源:2017届甘肃兰州一中高三9月月考数学(文)试卷(解析版) 题型:选择题
设集合A={x|x>a},集合B={-1,1,2},若A∩B=B,则实数a的取值范围是( )
A.(1,+∞) B.(-∞,1) C.(-1,+∞) D.(-∞,-1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com