
分析 (1)通过an+1=an2-an+1与an作差,结合完全平方公式即得结论;
(2)利用数学归纳法来证明:验证n=2时命题成立;当n=k时假设${2^{{2^{k-1}}}}<{a_{k+1}}-1<{2^{2^k}}$成立,通过放缩可知当n=k+1时${2^{2^k}}<{a_{k+2}}-1<{2^{{2^{k+1}}}}$,进而可得结论;
(3)通过对an+1=an2-an+1变形、取倒数裂项可知$\frac{1}{a_n}=\frac{1}{{{a_n}-1}}-\frac{1}{{{a_{n+1}}-1}}$,进而并项相加计算可知${S_n}=1-\frac{1}{{{a_{n+1}}-1}}$,结合第(2)问即得结论.
解答 (1)解:∵an+1=an2-an+1,
∴${a_{n+1}}-{a_n}=a_n^2-2{a_n}+1={({{a_n}-1})^2}$,
又∵a1=2,
∴an+1>an,∴an+2>an;
(2)证明:这里用数学归纳法来证明:
n=2时,${2^2}<{a_3}-1<{2^4}$成立;
当n=k时,假设${2^{{2^{k-1}}}}<{a_{k+1}}-1<{2^{2^k}}$成立,
则当n=k+1时,${a_{k+2}}=a_{k+1}^2-{a_{k+1}}+1={a_{k+1}}({{a_{k+1}}-1})+1≥({{2^{{2^{k-1}}}}+1})({{2^{{2^{k-1}}}}+2})+1={2^{2^k}}+2•{2^{{2^{k-1}}}}+3>{2^{2^k}}+1$,${a_{k+2}}=a_{k+1}^2-{a_{k+1}}+1={a_{k+1}}({{a_{k+1}}-1})+1≤{2^{2^k}}({{2^{2^k}}-1})+1={2^{{2^{k+1}}}}-{2^{2^k}}+1<{2^{{2^{k+1}}}}+1$,
∴${2^{2^k}}<{a_{k+2}}-1<{2^{{2^{k+1}}}}$,
综上可知:${2^{{2^{n-1}}}}<{a_{n+1}}-1<{2^{2^n}}$;
(3)解:∵an+1=an2-an+1,
∴an+1-1=an(an-1),
∴$\frac{1}{a_n}=\frac{1}{{{a_n}-1}}-\frac{1}{{{a_{n+1}}-1}}$,
利用并项相加法,计算可知${S_n}=1-\frac{1}{{{a_{n+1}}-1}}$,
根据第(2)问,$\frac{1}{{{2^{2^n}}}}<\frac{1}{{{a_{n+1}}-1}}<\frac{1}{{{2^{{2^{n-1}}}}}}$,
∴$\lim_{n→∞}{S_n}=1$.
点评 本题是一道关于数列与不等式的综合题,考查数学归纳法、裂项相消法,注意解题方法的积累,属于中档题.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:解答题
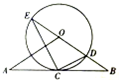 如图,直线AB经过圆O上的点C,并且OA=OB,CA=CB,圆O交直线OB于点E、D,连接EC、CD.
如图,直线AB经过圆O上的点C,并且OA=OB,CA=CB,圆O交直线OB于点E、D,连接EC、CD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
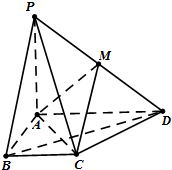 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AB⊥AD,BC=$\frac{2\sqrt{3}}{3}$,AB=1,BD=PA=2,M 为PD的中点.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AB⊥AD,BC=$\frac{2\sqrt{3}}{3}$,AB=1,BD=PA=2,M 为PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
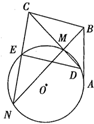 如图,BA与圆O相切,切点为A,割线BN与圆O分别交于点M,N,若BA=BC,连接CM并延长,交圆O于点D,割线CN与圆O的另一个交点为E.
如图,BA与圆O相切,切点为A,割线BN与圆O分别交于点M,N,若BA=BC,连接CM并延长,交圆O于点D,割线CN与圆O的另一个交点为E.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com