
分析 去绝对值号得出与原方程有4个根等价于x2-2kx-4k=0在[-2,+∞)上有两解,x2+2kx+4k=0在(-∞,-2)上有两解,根据二次函数的性质列出不等式组解出k的范围.
解答 解:当x≥-2时,x2-2kx-4k=0,
当x<-2时,x2+2kx+4k=0,
∵关于x的方程x2=2k|x+2|有四个不同的实根,
∴关于x的方程x2-2kx-4k=0在[-2,+∞)上有两解,
关于x的方程x2+2kx+4k=0在(-∞,-2)上有两解.
∴$\left\{\begin{array}{l}{4{k}^{2}+16k>0}\\{k>-2}\\{4+4k-4k>0}\\{4{k}^{2}-16k>0}\\{-k<-2}\\{4-4k+4k>0}\end{array}\right.$,解得k>4.
故答案为:(4,+∞).
点评 本题考查了二次函数的性质,根的个数判断,不等式的解法,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$cos5° | B. | -$\sqrt{2}$cos5° | C. | -$\sqrt{2}$sin5° | D. | $\sqrt{2}$sin5° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 手工社 | 摄影社 | 总计 | |
| 女生 | 6 | ||
| 男生 | 42 | ||
| 总计 | 30 | 60 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
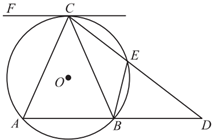 如图,已知CF是圆O的切线,C为切点,弦AB∥CF,E为圆周上一点,CE交AB的延长线于点D,弧$\widehat{AB}$=弧$\widehat{BC}$.求证:
如图,已知CF是圆O的切线,C为切点,弦AB∥CF,E为圆周上一点,CE交AB的延长线于点D,弧$\widehat{AB}$=弧$\widehat{BC}$.求证:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 女 | 男 | 总计 | |
| 喜欢 | 40 | 20 | 60 |
| 不喜欢 | 20 | 30 | 50 |
| 总计 | 60 | 50 | 110 |
| (K2≥k) | 0.100 | 0.010 | 0.001 |
| k | 2.706 | 6.635 | 10.828 |
| A. | 有99%以上的把握认为“喜欢该电视剧与性别无关” | |
| B. | 有99%以上的把握认为“喜欢该电视剧与性别有关” | |
| C. | 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关” | |
| D. | 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关” |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
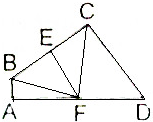 如图所示,四边形ABCD中,AB=1,AD=7,BC=CD=5,∠BAD=∠BCD=90°.
如图所示,四边形ABCD中,AB=1,AD=7,BC=CD=5,∠BAD=∠BCD=90°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届甘肃兰州一中高三9月月考数学(理)试卷(解析版) 题型:选择题
设集合A={x|x>a},集合B={-1,1,2},若A∩B=B,则实数a的取值范围是( )
A.(1,+∞) B.(-∞,1) C.(-1,+∞) D.(-∞,-1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com