
| ���� | ������ | �ܼ� | |
| ����/�� | 42 | 8 | 50 |
| ��/�� | 28 | 22 | 50 |
| �ܼ�/�� | 70 | 30 | 100 |
| P��K2��k�� | 0.100 | 0.050 | 0.010 | 0.001 |
| k | 2.706 | 3.843 | 6.635 | 10.828 |
���� ������2��2���������������ٽ�ֵ�Ĺ�ʽ������۲�ֵ�����ù۲�ֵͬ�ٽ�ֵ�����бȽϣ�K2��9.333��6.635������90%������Ϊ������Խ�����ͨ�����Ƿ����⡱���Ա��йأ�
������������������ε�ȡֵΪ1��2��3��4��5���ֱ��������ʣ��г��ֲ��У�������ѧ������ʽ���E��X����
��� �⣺������2��2��������֪��K2=$\frac{n��ad-bc��^{2}}{��a+b����c+d����a+c����b+d��}$=$\frac{100����42��22-8��28��^{2}}{50��50��70��30}$��9.333��6.635��
����90%������Ϊ������Խ�����ͨ�����Ƿ����⡱���Ա��йأ�
������������������ε�ȡֵΪ1��2��3��4��5��
P����=1��=$\frac{4}{8}$��
P����=2��=$\frac{4}{8}$��$\frac{4}{7}$=$\frac{2}{7}$��
P����=3��=$\frac{4}{8}$��$\frac{3}{7}$��$\frac{4}{6}$=$\frac{1}{7}$��
P����=4��=$\frac{4}{8}$��$\frac{3}{7}$��$\frac{2}{6}$��$\frac{4}{5}$=$\frac{2}{35}$��
P����=5��=$\frac{4}{8}$��$\frac{3}{7}$��$\frac{2}{6}$��$\frac{1}{5}$��1=$\frac{1}{70}$��
����������������εķֲ��У�
| �� | 1 | 2 | 3 | 4 | 5 |
| P | $\frac{1}{2}$ | $\frac{2}{7}$ | $\frac{1}{7}$ | $\frac{2}{35}$ | $\frac{1}{70}$ |
���� ���⿼������Լ���֪ʶ�����ã�����ȴ��ֲ��ļ��㹫ʽ���ֲ��к���ѧ����������������ϵļ��㹫ʽ��������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{2}$cos5�� | B�� | -$\sqrt{2}$cos5�� | C�� | -$\sqrt{2}$sin5�� | D�� | $\sqrt{2}$sin5�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��C��D��ֱ��ΪAB�İ�Բ�ϵ�������ͬ�ĵ㣬AC��BD���ڵ�E����F����BD�ϣ��ҡ�ACD�ס�BCF��֤������ABC�ס�DFC��
��ͼ��C��D��ֱ��ΪAB�İ�Բ�ϵ�������ͬ�ĵ㣬AC��BD���ڵ�E����F����BD�ϣ��ҡ�ACD�ס�BCF��֤������ABC�ס�DFC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| �ֹ��� | ��Ӱ�� | �ܼ� | |
| �� | 6 | ||
| ���� | 42 | ||
| �ܼ� | 30 | 60 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
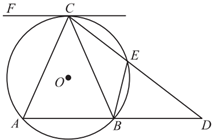 ��ͼ����֪CF��ԲO�����ߣ�CΪ�е㣬��AB��CF��EΪԲ����һ�㣬CE��AB���ӳ����ڵ�D����$\widehat{AB}$=��$\widehat{BC}$����֤��
��ͼ����֪CF��ԲO�����ߣ�CΪ�е㣬��AB��CF��EΪԲ����һ�㣬CE��AB���ӳ����ڵ�D����$\widehat{AB}$=��$\widehat{BC}$����֤���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com