
���� ��I����F��-c��0�������õ㵽ֱ�ߵľ��빫ʽ�������ʹ�ʽ�������Բ�Ļ������Ĺ�ϵ���ⷽ�̿ɵ�a��b�������õ���Բ���̣�
��������Բ���̿ɵý���F���꣬����ֱ��l1��б��Ϊ0��ֱ��l2��б�ʲ����ڣ����AB��CD�ij����ɵ��������ֱ��l1�ķ���Ϊy=k��x+$\frac{2\sqrt{2}}{3}$����������Բ���̣�����Τ�ﶨ���ͽ��뾶��ʽ���ɵ��ҳ�AB����k��Ϊ-$\frac{1}{k}$���ɵ�CD�ij������ı��ε������ʽS=$\frac{1}{2}$|AB|•|CD|�������������ɵ�k��ʽ�ӣ����û�Ԫ���ͻ�������ʽ�����ɵõ�S�ķ�Χ�������õ��������Сֵ��
��� �⣺��I����F��-c��0����
�ɵ�F��ֱ��ax+by=0�ľ���Ϊ$\frac{2\sqrt{5}}{5}$���ɵ�
$\frac{|-ac|}{\sqrt{{a}^{2}+{b}^{2}}}$=$\frac{2\sqrt{5}}{5}$����
��ԲE��������Ϊ$\frac{2\sqrt{2}}{3}$������e=$\frac{c}{a}$=$\frac{2\sqrt{2}}{3}$��
��a2-b2=c2����
�ɢ٢ڢ۽��a=1��b=$\frac{1}{3}$��c=$\frac{2\sqrt{2}}{3}$��
����Բ����Ϊx2+9y2=1��
��������Բ���̿ɵ�F��-$\frac{2\sqrt{2}}{3}$��0����
��ֱ��l1��б��Ϊ0��ֱ��l2��б�ʲ����ڣ�
��|AB|=2a=2��
��x=-c��������Բ���̿ɵ�y=��$\frac{{b}^{2}}{a}$=��$\frac{1}{9}$������|CD|=$\frac{2}{9}$��
�ɵ��ı���ACBD���Ϊ$\frac{1}{2}$��2��$\frac{2}{9}$=$\frac{2}{9}$��
��ֱ��l1��б��Ϊk���ɵ÷���Ϊy=k��x+$\frac{2\sqrt{2}}{3}$����
������Բ����x2+9y2=1���ɵã�1+9k2��x2+12$\sqrt{2}$k2x+8k2-1=0��
��A��x1��y1����B��x2��y2�����ɵ�x1+x2=-$\frac{12\sqrt{2}{k}^{2}}{1+9{k}^{2}}$��
����Բ�Ľ��뾶��ʽ�ɵ�|AB|=��a+ex1��+��a+ex2��=2a+e��x1+x2��
=2-$\frac{2\sqrt{2}}{3}$��$\frac{12\sqrt{2}{k}^{2}}{1+9{k}^{2}}$=$\frac{2��1+{k}^{2}��}{1+9{k}^{2}}$��
��k��Ϊ-$\frac{1}{k}$���ɵ�|CD|=$\frac{2��1+\frac{1}{{k}^{2}}��}{1+\frac{9}{{k}^{2}}}$��
���ı���ACBD���ΪS=$\frac{1}{2}$|AB|•|CD|=2•$\frac{2+{k}^{2}+\frac{1}{{k}^{2}}}{82+9��{k}^{2}+\frac{1}{{k}^{2}}��}$��
��t=k2+$\frac{1}{{k}^{2}}$��t��2������S=2•$\frac{2+t}{82+9t}$=2•$\frac{1}{9+\frac{64}{2+t}}$��
��t��2�ɵ�2+t��4��0��$\frac{64}{2+t}$��16������
$\frac{1}{25}$��$\frac{1}{9+\frac{64}{2+t}}$��$\frac{1}{9}$��
��$\frac{2}{25}$��S��$\frac{2}{9}$��
���Ͽɵã�$\frac{2}{25}$��S��$\frac{2}{9}$��
��ֱ��l1��б��Ϊ��1ʱ���ı���ACBD���������СֵΪ$\frac{2}{25}$��
���� ���⿼����Բ�ķ��̵���ע�����������ʹ�ʽ������ֱ�ߺ���Բ�ཻ�ҳ�����ע������ֱ�߷��̺���Բ���̣�����Τ�ﶨ���ͽ��뾶��ʽ�������������ʽ�Ͳ���ʽ�����ʵ����ã��������������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 С���ڡ�ŷ�������Ρ��������ж�ij����������ľ��ۼ������£��ֻ��Ƹý����������ͼ��ͼ��ʾ��������ֽ��С�����εı߳�Ϊ1����С�����ƵĽ���������Ϊ��������
С���ڡ�ŷ�������Ρ��������ж�ij����������ľ��ۼ������£��ֻ��Ƹý����������ͼ��ͼ��ʾ��������ֽ��С�����εı߳�Ϊ1����С�����ƵĽ���������Ϊ��������| A�� | 16+8�� | B�� | 64+8�� | C�� | 64+$\frac{8��}{3}$ | D�� | 16+$\frac{8��}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-2��-1�� | B�� | ��-1��+�ޣ� | C�� | ��-1��2�� | D�� | ��-�ޣ�+�ޣ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
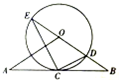 ��ͼ��ֱ��AB����ԲO�ϵĵ�C������OA=OB��CA=CB��ԲO��ֱ��OB�ڵ�E��D������EC��CD��
��ͼ��ֱ��AB����ԲO�ϵĵ�C������OA=OB��CA=CB��ԲO��ֱ��OB�ڵ�E��D������EC��CD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
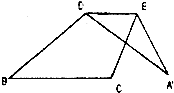 ��ͼ������ABC����������λ��DE�۵���A�䵽��A�䣬����C=120�㣬��A=26�㣬���A��DB�Ķ�����112�㣮
��ͼ������ABC����������λ��DE�۵���A�䵽��A�䣬����C=120�㣬��A=26�㣬���A��DB�Ķ�����112�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ���� | ������ | �ܼ� | |
| ����/�� | 42 | 8 | 50 |
| ��/�� | 28 | 22 | 50 |
| �ܼ�/�� | 70 | 30 | 100 |
| P��K2��k�� | 0.100 | 0.050 | 0.010 | 0.001 |
| k | 2.706 | 3.843 | 6.635 | 10.828 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
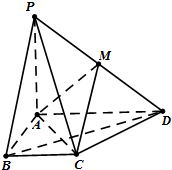 ��ͼ��������P-ABCD�У�PA��ƽ��ABCD��AD��BC��AB��AD��BC=$\frac{2\sqrt{3}}{3}$��AB=1��BD=PA=2��M ΪPD���е㣮
��ͼ��������P-ABCD�У�PA��ƽ��ABCD��AD��BC��AB��AD��BC=$\frac{2\sqrt{3}}{3}$��AB=1��BD=PA=2��M ΪPD���е㣮�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com