
分析 (1)求出双曲线的离心率,然后求解双曲线方程,即可得到双曲线的虚轴的长.
(2)求出双曲线的渐近线方程,设出圆的圆心与半径,列出方程求解即可.
解答 解:(1)方程2x2-5x+2=0的根,分别为:$\frac{1}{2}$和2,双曲线mx2-3y2=3m的离心率e是方程2x2-5x+2=0的一个根,可得e=2,
双曲线mx2-3y2=3m化为:$\frac{{x}^{2}}{3}-\frac{{y}^{2}}{m}=1$,可得a=$\sqrt{3}$,b=$\sqrt{m}$,c=2$\sqrt{3}$.
所以:12=3+m,解得m=9.
(2)由(1)可知双曲线方程为:$\frac{{x}^{2}}{3}-\frac{{y}^{2}}{9}=1$,
双曲线的渐近线方程为:y=$±\sqrt{3}x$.
设圆的圆心为:(t,0),t∈(0,$\sqrt{3}$)则圆的半径为:$\sqrt{3}-t$,
圆与双曲线及双曲线的两渐近线都相切,可得:$\frac{|\sqrt{3}t|}{\sqrt{1+3}}=\sqrt{3}-t$,
解得t=4$\sqrt{3}$-6.
圆的圆心坐标为:(4$\sqrt{3}-$6,0)或(6-4$\sqrt{3}$,0)半径为:6-3$\sqrt{3}$.
所求圆的方程为:(x+6-4$\sqrt{3}$)2+y2=(6-3$\sqrt{3}$)2.或(x-6+4$\sqrt{3}$)2+y2=(6-3$\sqrt{3}$)2.
点评 本题考查双曲线的方程的求法,双曲线的简单性质的应用,圆与双曲线的位置关系的应用,考查计算能力以及转化思想的应用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
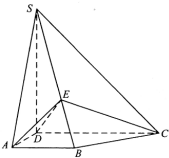 如图,四棱锥S-ABCD中,SD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,DC=SD=2,E为棱SB上的一点,二面角D-EC-B等于90°.
如图,四棱锥S-ABCD中,SD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,DC=SD=2,E为棱SB上的一点,二面角D-EC-B等于90°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 手工社 | 摄影社 | 总计 | |
| 女生 | 6 | ||
| 男生 | 42 | ||
| 总计 | 30 | 60 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 有40名高校应届毕业生参加某招工单位应聘,其中甲组20人学历为硕士研究生,乙组20人学历是本科,他们首先参加笔试,统计考试成绩得到的茎叶图如图(满分100分),如果成绩在86分以上(含86分)才可以进入面试阶段
有40名高校应届毕业生参加某招工单位应聘,其中甲组20人学历为硕士研究生,乙组20人学历是本科,他们首先参加笔试,统计考试成绩得到的茎叶图如图(满分100分),如果成绩在86分以上(含86分)才可以进入面试阶段| 本科生 | 研究生 | 合计 | |
| 能参加面试 | |||
| 不能参加面试 | |||
| 合计 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6,635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 女 | 男 | 总计 | |
| 喜欢 | 40 | 20 | 60 |
| 不喜欢 | 20 | 30 | 50 |
| 总计 | 60 | 50 | 110 |
| (K2≥k) | 0.100 | 0.010 | 0.001 |
| k | 2.706 | 6.635 | 10.828 |
| A. | 有99%以上的把握认为“喜欢该电视剧与性别无关” | |
| B. | 有99%以上的把握认为“喜欢该电视剧与性别有关” | |
| C. | 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关” | |
| D. | 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关” |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com