
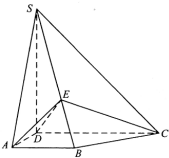
 如图,四棱锥S-ABCD中,SD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,DC=SD=2,E为棱SB上的一点,二面角D-EC-B等于90°.
如图,四棱锥S-ABCD中,SD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,DC=SD=2,E为棱SB上的一点,二面角D-EC-B等于90°.分析 (Ⅰ)连接BD,取DC的中点G,连接BG,利用已知及其直角三角形的判定可得△DBC为直角三角形,故BC⊥BD.再利用线面垂直的性质定理与判定定理可得:BC⊥SD,BC⊥DE.作BK⊥EC,K为垂足,利用面面垂直的性质定理可得:BK⊥平面EDC,BK⊥DE,进而得出DE⊥平面SBC.
(Ⅱ) 由DE⊥平面SBC,DE⊥EC,DE⊥SB,利用勾股定理、真假三角形的面积计算公式计算即可得出证明.
(III)由(II)知:$AE=\sqrt{{(\frac{1}{3}SA)}^{2}+{(\frac{2}{3}AB)}^{2}}=1$,可得△ADE为等腰三角形.取ED中点F,连接AF,AF⊥DE.连接FG,则FG∥EC,FG⊥DE.可得∠AFG是二面角A-DE-C的平面角.△AFG中,利用余弦定理即可得出.
解答 (Ⅰ)证明:连接BD,取DC的中点G,连接BG,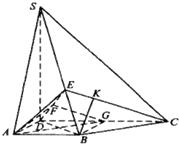
由此知DG=GC=BG=1,即△DBC为直角三角形,故BC⊥BD.
又SD⊥平面ABCD,∴BC⊥SD,∴BC⊥平面BDS,BC⊥DE.
作BK⊥EC,K为垂足,∵平面EDC⊥平面SBC,
∴BK⊥平面EDC,BK⊥DE,DE与平面SBC内的两条相交直线BK、BC都垂直.
∴DE⊥平面SBC
(Ⅱ)证明:由DE⊥平面SBC,DE⊥EC,DE⊥SB,
$SB=\sqrt{S{D}^{2}+D{B}^{2}}=\sqrt{6},DE=\frac{SD•DB}{SB}=\frac{2}{\sqrt{3}}$,$EB=\sqrt{D{B}^{2}-D{E}^{2}}=\frac{\sqrt{6}}{3},SE=SB-EB=\frac{2\sqrt{6}}{3}$,
∴$EB=\sqrt{D{B}^{2}-D{E}^{2}}=\frac{\sqrt{6}}{3},SE=SB-EB=\frac{2\sqrt{6}}{3}$.
(Ⅲ)解:由(II)知:$AE=\sqrt{{(\frac{1}{3}SA)}^{2}+{(\frac{2}{3}AB)}^{2}}=1$,又AD=1.
∴△ADE为等腰三角形.
取ED中点F,连接AF,则$AF⊥DE,AF=\sqrt{A{D}^{2}-D{F}^{2}}=\frac{\sqrt{6}}{3}$.
连接FG,则FG∥EC,FG⊥DE.∴∠AFG是二面角A-DE-C的平面角.
连接AG,AG=$\sqrt{2},FG=\sqrt{D{G}^{2}-D{F}^{2}}=\frac{\sqrt{6}}{3},cos∠AFG=\frac{A{F}^{2}+F{G}^{2}-A{G}^{2}}{2•AF•FG}=-\frac{1}{2}$,
∴二面角A-DE-C的余弦值为$-\frac{1}{2}$.
点评 本题考查了空间位置关系空间角、三角形中位线定理、等腰三角形的性质、勾股定理、余弦定理,考查了空间想象能力、推理能力与计算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,在△ABC中,CD是∠ACB的角平分线,△ADC的外接圆交线段BC于点E,BE=3AD.
如图所示,在△ABC中,CD是∠ACB的角平分线,△ADC的外接圆交线段BC于点E,BE=3AD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,-1) | B. | (-1,+∞) | C. | (-1,2) | D. | (-∞,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
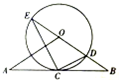 如图,直线AB经过圆O上的点C,并且OA=OB,CA=CB,圆O交直线OB于点E、D,连接EC、CD.
如图,直线AB经过圆O上的点C,并且OA=OB,CA=CB,圆O交直线OB于点E、D,连接EC、CD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
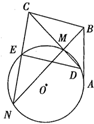 如图,BA与圆O相切,切点为A,割线BN与圆O分别交于点M,N,若BA=BC,连接CM并延长,交圆O于点D,割线CN与圆O的另一个交点为E.
如图,BA与圆O相切,切点为A,割线BN与圆O分别交于点M,N,若BA=BC,连接CM并延长,交圆O于点D,割线CN与圆O的另一个交点为E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com