
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 3 |
分析 利用射影定理,确定c=$\frac{1}{2}$|OA|,可得∠AOF=60°,$\frac{b}{a}$=tan60°=$\sqrt{3}$,即可求出双曲线的离心率.
解答 解:由射影定理可得,|OF|2=|OH|•|OA|,
∵$\overrightarrow{OA}$=4$\overrightarrow{OH}$,∴c=$\frac{1}{2}$|OA|,
∴∠AOF=60°,
∴$\frac{b}{a}$=tan60°=$\sqrt{3}$,
∴c=$\sqrt{{a}^{2}+{b}^{2}}$=2a,
∴e=$\frac{c}{a}$=2,
故选:C.
点评 本题考查双曲线的离心率,考查射影定理,考查学生的计算能力,属于中档题.


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 60种 | B. | 70种 | C. | 75种 | D. | 150种 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{1}{5}$i | C. | -$\frac{1}{3}$ | D. | -$\frac{1}{3}$i |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在半球O的直径AB的延长线上取一点P,作PC的切半圆O于点C,又经过P任作一直线交半圆O于点M、N,过C作CD⊥AB,垂足为D
如图,在半球O的直径AB的延长线上取一点P,作PC的切半圆O于点C,又经过P任作一直线交半圆O于点M、N,过C作CD⊥AB,垂足为D查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
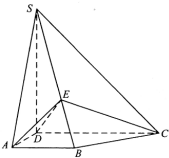 如图,四棱锥S-ABCD中,SD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,DC=SD=2,E为棱SB上的一点,二面角D-EC-B等于90°.
如图,四棱锥S-ABCD中,SD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,DC=SD=2,E为棱SB上的一点,二面角D-EC-B等于90°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com