
 如图所示,在△ABC中,CD是∠ACB的角平分线,△ADC的外接圆交线段BC于点E,BE=3AD.
如图所示,在△ABC中,CD是∠ACB的角平分线,△ADC的外接圆交线段BC于点E,BE=3AD.分析 (1)证明△BDE∽△BCA,则$\frac{BE}{BA}=\frac{DE}{CA}$,利用三角形的角平分线的性质,结合条件,得出AB=3AC;
(2)根据割线定理得BD•BA=BE•BC,所以BC=12,EC=BC-BE=3,证明DE∥AC,在等腰梯形ACED中,求得CD的长.
解答 (1)证明:因为四边形ACED为圆内接四边形,所以∠BDE=∠BCA,
又∠DBE=∠CBA,所以△BDE∽△BCA,则$\frac{BE}{BA}=\frac{DE}{CA}$,
在圆内接四边形ACED中,CD是∠ACE的平分线,
所以DE=AD,$\frac{BE}{BA}=\frac{AD}{CA}$,
而BE=3AD,所以BA=3CA,即AB=3AC.
(2)解:由(1)得AB=3AC=12,而AD=3,所以DE=3,BD=9,BE=3AD=9,
根据割线定理得BD•BA=BE•BC,所以BC=12,EC=BC-BE=3,
在圆内接四边形ACED中,由于AD=EC,所以∠ACD=∠EDC,DE∥AC,
在等腰梯形ACED中,求得$CD=\sqrt{21}$.
点评 本题考查三角形相似的判定与性质,考查角平分线的性质,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 60种 | B. | 70种 | C. | 75种 | D. | 150种 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{9}$+y2=1 | B. | $\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{81}$=1 | ||
| C. | $\frac{{x}^{2}}{9}$+y2=1或$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{81}$=1 | D. | $\frac{{x}^{2}}{9}$+y2=1或$\frac{{x}^{2}}{81}$+$\frac{{y}^{2}}{9}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
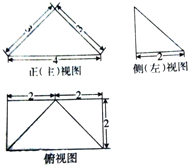
| A. | 四个侧面的面积相等 | |
| B. | 四个侧面中任意两个的面积不相等 | |
| C. | 四个侧面中面积最大的侧面的面积为6 | |
| D. | 四个侧面中面积最大的侧面的面积为2$\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
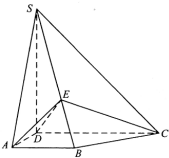 如图,四棱锥S-ABCD中,SD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,DC=SD=2,E为棱SB上的一点,二面角D-EC-B等于90°.
如图,四棱锥S-ABCD中,SD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,DC=SD=2,E为棱SB上的一点,二面角D-EC-B等于90°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 有40名高校应届毕业生参加某招工单位应聘,其中甲组20人学历为硕士研究生,乙组20人学历是本科,他们首先参加笔试,统计考试成绩得到的茎叶图如图(满分100分),如果成绩在86分以上(含86分)才可以进入面试阶段
有40名高校应届毕业生参加某招工单位应聘,其中甲组20人学历为硕士研究生,乙组20人学历是本科,他们首先参加笔试,统计考试成绩得到的茎叶图如图(满分100分),如果成绩在86分以上(含86分)才可以进入面试阶段| 本科生 | 研究生 | 合计 | |
| 能参加面试 | |||
| 不能参加面试 | |||
| 合计 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6,635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com