
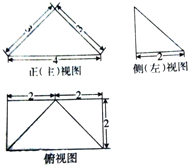
| A. | 四个侧面的面积相等 | |
| B. | 四个侧面中任意两个的面积不相等 | |
| C. | 四个侧面中面积最大的侧面的面积为6 | |
| D. | 四个侧面中面积最大的侧面的面积为2$\sqrt{5}$ |
分析 如图所示,四棱锥P-ABCD中,侧面PAD⊥底面ABCD,PA=PD.分别取AD,BC的中点O,E,连接PO,OE,PE,则PO⊥AD,PE⊥BC.利用三角形面积计算公式即可得出.
解答 解:如图所示,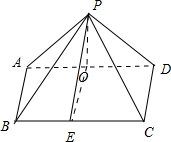
四棱锥P-ABCD中,侧面PAD⊥底面ABCD,PA=PD.
分别取AD,BC的中点O,E,连接PO,OE,PE,
则PO⊥AD,PE⊥BC.
PO=$\sqrt{{3}^{2}-{2}^{2}}$=$\sqrt{5}$,PE=$\sqrt{(\sqrt{5})^{2}+{2}^{2}}$=3.
S侧面PAD=$\frac{1}{2}×2×\sqrt{5}$=$\sqrt{5}$,S△PAB=S△PCD=$\frac{1}{2}×3×$2=3,
S△PBC=$\frac{1}{2}×4×3$=6.
因此四个侧面中面积最大的侧面的面积为△PBC的面积6.
故选:C.
点评 本题考查了四棱锥的三视图、线面垂直的性质、三角形面积计算公式,考查了推理能力与计算能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
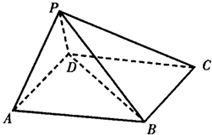 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,∠BAD=60°,AB=4,AD=2,侧棱PB=$\sqrt{15}$,PD=$\sqrt{3}$.
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,∠BAD=60°,AB=4,AD=2,侧棱PB=$\sqrt{15}$,PD=$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 小明在“欧洲七日游”的游玩中对某著名建筑物的景观记忆犹新,现绘制该建筑物的三视图如图所示,若网格纸上小正方形的边长为1,则小明绘制的建筑物的体积为( )
小明在“欧洲七日游”的游玩中对某著名建筑物的景观记忆犹新,现绘制该建筑物的三视图如图所示,若网格纸上小正方形的边长为1,则小明绘制的建筑物的体积为( )| A. | 16+8π | B. | 64+8π | C. | 64+$\frac{8π}{3}$ | D. | 16+$\frac{8π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在等腰梯形ABCD中,AB∥CD,AD=DC=CB=CF=1,∠ABC=60°,四边形ACFE为矩形,点M为线段EF中点,平面ACFE⊥平面ABCD.
如图,在等腰梯形ABCD中,AB∥CD,AD=DC=CB=CF=1,∠ABC=60°,四边形ACFE为矩形,点M为线段EF中点,平面ACFE⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,在△ABC中,CD是∠ACB的角平分线,△ADC的外接圆交线段BC于点E,BE=3AD.
如图所示,在△ABC中,CD是∠ACB的角平分线,△ADC的外接圆交线段BC于点E,BE=3AD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,-1) | B. | (-1,+∞) | C. | (-1,2) | D. | (-∞,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
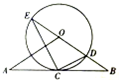 如图,直线AB经过圆O上的点C,并且OA=OB,CA=CB,圆O交直线OB于点E、D,连接EC、CD.
如图,直线AB经过圆O上的点C,并且OA=OB,CA=CB,圆O交直线OB于点E、D,连接EC、CD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
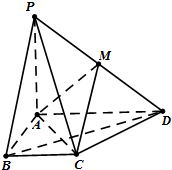 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AB⊥AD,BC=$\frac{2\sqrt{3}}{3}$,AB=1,BD=PA=2,M 为PD的中点.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AB⊥AD,BC=$\frac{2\sqrt{3}}{3}$,AB=1,BD=PA=2,M 为PD的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com