
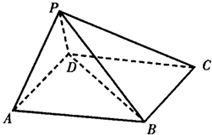
 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,∠BAD=60°,AB=4,AD=2,侧棱PB=$\sqrt{15}$,PD=$\sqrt{3}$.
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,∠BAD=60°,AB=4,AD=2,侧棱PB=$\sqrt{15}$,PD=$\sqrt{3}$.分析 (1)利用余弦定理求出BD.推出△ABD是直角三角形,AD⊥BD,然后证明PD⊥BD.可证明BD⊥平面PAD.
(2)说明平面PAD⊥平面ABCD.作PE⊥AD于E,说明∠PDE是PD与底面BCD所成的角,作EF⊥BC于F,连PF,说明∠PFE是二面角P-BC-A的平面角.然后求解二面角P-BC-A所成的平面角的正切值.
解答 (本小题满分12分)
解 (1)由已知AB=4,AD=2,∠BAD=60°,
得BD2=AD2+AB2-2AD•ABcos60°=4+16-2×2×4×$\frac{1}{2}$=12.
AB2=AD2+BD2,
∴△ABD是直角三角形,∠ADB=90°,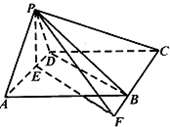
即AD⊥BD
在△PDB中,PD=$\sqrt{3}$,PB=$\sqrt{15}$,BD=$\sqrt{12}$,
∴PB2=PD2+BD2,故得PD⊥BD.
又PD∩AD=D,∴BD⊥平面PAD.
(2)∵BD⊥平面PAD,BD?平面ABCD,
∴平面PAD⊥平面ABCD.
作PE⊥AD于E,又PE平面PAD,∴PE⊥平面ABCD,
∴∠PDE是PD与底面BCD所成的角,∴∠PDE=60°,
∴PE=PDsin60°=$\sqrt{3}$•$\frac{{\sqrt{3}}}{2}$=$\frac{3}{2}$.
作EF⊥BC于F,连PF,则PF⊥BC,∴∠PFE是二面角P-BC-A的平面角.
又EF=BD=$\sqrt{12}$,∴在Rt△PEF中,
tan∠PFE=$\frac{PE}{EF}$=$\frac{{\frac{3}{2}}}{{2\sqrt{3}}}$=$\frac{{\sqrt{3}}}{4}$.
故二面角P-BC-A所成的平面角的正切值为$\frac{{\sqrt{3}}}{4}$.
点评 本题考查直线与平面垂直,平面与平面垂直,直线与平面市场价以及二面角,考查计算能力空间想象能力.


科目:高中数学 来源: 题型:解答题
| 是否为会员 性别 | 是 | 否 |
| 男生 | 20 | 5 |
| 女生 | 10 | 15 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 喜爱打篮球 | 不喜爱打篮球 | 合计 | |
| 男生 | 5 | ||
| 女生[来 | 10 | ||
| 合计 | 50 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 60种 | B. | 70种 | C. | 75种 | D. | 150种 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在半球O的直径AB的延长线上取一点P,作PC的切半圆O于点C,又经过P任作一直线交半圆O于点M、N,过C作CD⊥AB,垂足为D
如图,在半球O的直径AB的延长线上取一点P,作PC的切半圆O于点C,又经过P任作一直线交半圆O于点M、N,过C作CD⊥AB,垂足为D查看答案和解析>>
科目:高中数学 来源: 题型:选择题
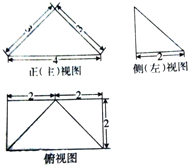
| A. | 四个侧面的面积相等 | |
| B. | 四个侧面中任意两个的面积不相等 | |
| C. | 四个侧面中面积最大的侧面的面积为6 | |
| D. | 四个侧面中面积最大的侧面的面积为2$\sqrt{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com