
分析 a1=1,a2=1,an+2=an+1+an(n∈N*).由{an}中各项按顺序排列可得:1,1,2,3,5,8,13,21,34,55,89,144,233,….{an}中各项除以4所得余数按原顺序构成的数列记为{bn},分别为:1,1,2,3,1,0,1,2,3,1,0,1,…,可得其周期,即可得出.
解答 解:a1=1,a2=1,an+2=an+1+an(n∈N*).
∴{an}中各项按顺序排列可得:1,1,2,3,5,8,13,21,34,55,89,144,233,…,
{an}中各项除以4所得余数按原顺序构成的数列记为{bn},
分别为:1,1,2,3,1,0,1,2,3,1,0,1,…,
从上面可以看出:{bn}从第二项开始是周期为5的数列,
∴b2015=b1+402×5+4=b5=1.
故答案为:1.
点评 本题考查了斐波那契数列的通项公式及其性质、整除的性质,考查了推理能力、猜想归纳与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
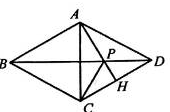 如图,四边形ABCD中,AB=AC=AD,AH⊥CD于H,BD交AH于P,且PC⊥BC
如图,四边形ABCD中,AB=AC=AD,AH⊥CD于H,BD交AH于P,且PC⊥BC查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3+4i | B. | $\frac{3}{5}$+$\frac{4}{5}$i | C. | $\frac{3}{15}$-$\frac{4}{15}$i | D. | $\frac{3}{25}$-$\frac{4}{25}$i |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
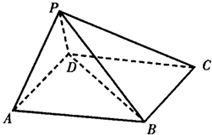 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,∠BAD=60°,AB=4,AD=2,侧棱PB=$\sqrt{15}$,PD=$\sqrt{3}$.
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,∠BAD=60°,AB=4,AD=2,侧棱PB=$\sqrt{15}$,PD=$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=ex+e-x | B. | f(x)=ex-e-x | C. | f(x)=x|x| | D. | f(x)=cos(x-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com