
| 喜爱打篮球 | 不喜爱打篮球 | 合计 | |
| 男生 | 5 | ||
| 女生[来 | 10 | ||
| 合计 | 50 |
分析 (1)根据抽到喜爱打篮球的概率求出喜爱打篮球的总人数,由此补充列联表即可;
(2)根据列联表计算观测值K2,对照临界值表即可得出结论.
解答 解:(1)在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为$\frac{3}{5}$,
所以喜爱打篮球的人数有50×$\frac{3}{5}$=30;
由此补充列联表如下:
| 喜爱打篮球 | 不喜爱打篮球 | 合计 | |
| 男生 | 20 | 5 | 25 |
| 女生 | 10 | 15 | 25 |
| 合计 | 30 | 20 | 50 |
点评 本题考查了列联表与独立性检验的应用问题,是基础题目.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{17π}{6}$ | B. | $\frac{17π}{3}$ | C. | 5π | D. | $\frac{13π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 态度 | 积极支持企业改革 | 不太支持企业改革 | 总计 |
| 工作积极 | 54 | 40 | 94 |
| 工作一般 | 32 | 63 | 95 |
| 总计 | 86 | 103 | 189 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
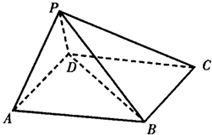 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,∠BAD=60°,AB=4,AD=2,侧棱PB=$\sqrt{15}$,PD=$\sqrt{3}$.
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,∠BAD=60°,AB=4,AD=2,侧棱PB=$\sqrt{15}$,PD=$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
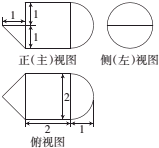
 小明在“欧洲七日游”的游玩中对某著名建筑物的景观记忆犹新,现绘制该建筑物的三视图如图所示,若网格纸上小正方形的边长为1,则小明绘制的建筑物的体积为( )
小明在“欧洲七日游”的游玩中对某著名建筑物的景观记忆犹新,现绘制该建筑物的三视图如图所示,若网格纸上小正方形的边长为1,则小明绘制的建筑物的体积为( )| A. | 16+8π | B. | 64+8π | C. | 64+$\frac{8π}{3}$ | D. | 16+$\frac{8π}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com