
分析 由题意可知O,A,P,B四点共圆,求出OP中点坐标,由两点间的距离公式求出|OP|,得到以OP为直径的圆的方程,与已知圆的方程作差得答案.
解答 解:如图,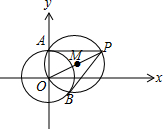
∵PA,PB是圆x2+y2=1的两条切线,∴O,A,P,B四点共圆,
OP中点M(1,$\frac{1}{2}$),|OP|=$\sqrt{{2}^{2}+{1}^{2}}=\sqrt{5}$,
则以M为圆心,以OP为直径的圆的方程为$(x-1)^{2}+(y-\frac{1}{2})^{2}=(\frac{\sqrt{5}}{2})^{2}$,
整理得:x2+y2-2x-y=0.
联立$\left\{\begin{array}{l}{{x}^{2}+{y}^{2}=1①}\\{{x}^{2}+{y}^{2}-2x-y=0②}\end{array}\right.$,①-②得:2x+y-1=0.
∴直线AB方程为2x+y-1=0.
点评 本题考查直线与圆的位置关系的应用,训练了过圆的两切点的直线的求法,体现了数学转化思想方法,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 是否为会员 性别 | 是 | 否 |
| 男生 | 20 | 5 |
| 女生 | 10 | 15 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 类别 | 数优 | 数差 | 总计 |
| 外优 | 34 | 17 | 51 |
| 外差 | 15 | 19 | 34 |
| 总计 | 49 | 36 | 85 |
| A. | 10.3 | B. | 8 | C. | 4.25 | D. | 9.3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 喜爱打篮球 | 不喜爱打篮球 | 合计 | |
| 男生 | 5 | ||
| 女生[来 | 10 | ||
| 合计 | 50 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在半球O的直径AB的延长线上取一点P,作PC的切半圆O于点C,又经过P任作一直线交半圆O于点M、N,过C作CD⊥AB,垂足为D
如图,在半球O的直径AB的延长线上取一点P,作PC的切半圆O于点C,又经过P任作一直线交半圆O于点M、N,过C作CD⊥AB,垂足为D查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com