
分析 (1)通过联立S3=7=a1+a2+a3与a1+3,3a2,a3+4构成等差数列,可求出公比q,进而代入S3=7可求出首项,进而整理即得结论;
(2)通过(1)裂项可知$\frac{1}{b_n}$=$\frac{1}{n}$-$\frac{1}{n+1}$,进而并项相加、放缩即得结论.
解答 (1)解:∵数列{an}是等比数列,S3=7=a1+a2+a3,
又∵a1+3,3a2,a3+4构成等差数列,
∴6a2=a1+3+a3+4=a1+a3+(a1+a2+a3),即5a2=2a1+2a3,
记数列{an}的公比为q,则5a1q=2a1+2a1q2,
∴2q2-5q+2=0,即(2q-1)(q-2)=0,解得:q=2或q=$\frac{1}{2}$(舍),
又∴S3=7=a1(1+2+4),即a1=1,
∴数列{an}的通项公式an=2n-1;
(2)证明:由(1)可知bn=(n+1)log2an+1=n(n+1),
∵$\frac{1}{b_n}$=$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$,
∴$\frac{1}{b_1}+\frac{1}{b_2}+…\frac{1}{{{b_{n-1}}}}+\frac{1}{b_n}=1-\frac{1}{2}+…+\frac{1}{n}-\frac{1}{n+1}=1-\frac{1}{n+1}<1$.
点评 本题是一道关于数列与不等式的综合题,考查运算求解能力及裂项相消法,注意解题方法的积累,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3+4i | B. | $\frac{3}{5}$+$\frac{4}{5}$i | C. | $\frac{3}{15}$-$\frac{4}{15}$i | D. | $\frac{3}{25}$-$\frac{4}{25}$i |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
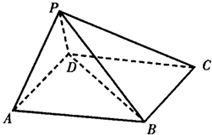 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,∠BAD=60°,AB=4,AD=2,侧棱PB=$\sqrt{15}$,PD=$\sqrt{3}$.
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,∠BAD=60°,AB=4,AD=2,侧棱PB=$\sqrt{15}$,PD=$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在等腰梯形ABCD中,AB∥CD,AD=DC=CB=CF=1,∠ABC=60°,四边形ACFE为矩形,点M为线段EF中点,平面ACFE⊥平面ABCD.
如图,在等腰梯形ABCD中,AB∥CD,AD=DC=CB=CF=1,∠ABC=60°,四边形ACFE为矩形,点M为线段EF中点,平面ACFE⊥平面ABCD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com