
���� �����ɵ�A�ļ�����Ϊ��4$\sqrt{2}$��$\frac{��}{4}$������ֱ֪��OA����ԭ�㣬��б��Ϊ$\frac{��}{4}$�����ɵó����̣�
����A�ļ�����Ϊ��4$\sqrt{2}$��$\frac{��}{4}$�������û�����ʽ��Ϊֱ�����꣬������C�IJ�������Ϊ$\left\{\begin{array}{l}x=1+\sqrt{2}cos��\\ y=\sqrt{2}sin��\end{array}\right.$����Ϊ������������ƽ����ϵ�ɵ���ͨ���̿ɵ�Բ��ΪC���뾶r���ɵ�|AM|min=|AC|-r��
��� �⣺�����ɵ�A�ļ�����Ϊ��4$\sqrt{2}$��$\frac{��}{4}$����
��$\frac{y}{x}=tan\frac{��}{4}$��
��ֱ��OA�ķ���Ϊ��y=x��
����A�ļ�����Ϊ��4$\sqrt{2}$��$\frac{��}{4}$������Ϊֱ������A��4��4����
������C�IJ�������Ϊ$\left\{\begin{array}{l}x=1+\sqrt{2}cos��\\ y=\sqrt{2}sin��\end{array}\right.$����Ϊ������������ƽ����ϵ�ɵ���ͨ���̣���x-1��2+y2=2��
��Բ��ΪC��1��0�����뾶Ϊ$\sqrt{2}$��
���ڵ�A��Բ�⣬��|AC|=5��
��|AM|min=5-$\sqrt{2}$��
���� ���⿼���˼�������ֱ������Ļ������������̻�Ϊ��ͨ���̡�����֮��ľ��빫ʽ��������������������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ʾ���ڡ�ABC�У�CD�ǡ�ACB�Ľ�ƽ���ߣ���ADC�����Բ���߶�BC�ڵ�E��BE=3AD��
��ͼ��ʾ���ڡ�ABC�У�CD�ǡ�ACB�Ľ�ƽ���ߣ���ADC�����Բ���߶�BC�ڵ�E��BE=3AD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{��}{6}$ | B�� | $\frac{��}{4}$ | C�� | $\frac{��}{3}$ | D�� | $\frac{��}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-2��-1�� | B�� | ��-1��+�ޣ� | C�� | ��-1��2�� | D�� | ��-�ޣ�+�ޣ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
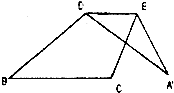 ��ͼ������ABC����������λ��DE�۵���A�䵽��A�䣬����C=120�㣬��A=26�㣬���A��DB�Ķ�����112�㣮
��ͼ������ABC����������λ��DE�۵���A�䵽��A�䣬����C=120�㣬��A=26�㣬���A��DB�Ķ�����112�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com