
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
分析 依题意可求tanα=$\frac{1}{3}$tanθ,利用两角和的正切函数公式,基本不等式可得,利用正切函数的图象和性质即可解得函数y=θ-α(0<θ<$\frac{π}{2}$)的最大值.
解答 解:依题意,$-\frac{π}{2}<y<\frac{π}{2}$,
$tanα=\frac{sinθ}{3cosθ}=\frac{1}{3}tanθ$,
故$tany=tan(θ-α)=\frac{{tanθ-\frac{tanθ}{3}}}{{1+\frac{{{{tan}^2}θ}}{3}}}$=$\frac{2}{3}•\frac{1}{{\frac{1}{tanθ}+\frac{tanθ}{3}}}≤\frac{{\sqrt{3}}}{3}$,
当且仅当$θ=\frac{π}{3}$时ymax=$\frac{π}{6}$,
故选:A.
点评 本题主要考查了任意角的三角函数的定义,两角和的正切函数公式,基本不等式,正切函数的图象和性质的综合应用,考查了数形结合思想和转化思想,考查了计算能力,属于中档题.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{10}$ | B. | 2$\sqrt{2}$ | C. | 4 | D. | $\frac{\sqrt{10}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{9}$+y2=1 | B. | $\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{81}$=1 | ||
| C. | $\frac{{x}^{2}}{9}$+y2=1或$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{81}$=1 | D. | $\frac{{x}^{2}}{9}$+y2=1或$\frac{{x}^{2}}{81}$+$\frac{{y}^{2}}{9}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若ξ~B(4,0.25),则Dξ=1 | |
| B. | “am2<bm2”是“a<b”的充分不必要条件 | |
| C. | 若p、q均为假命题,则“p且q”为假命题 | |
| D. | 命题“?x∈R,x2-x-1≤0”的否定是“?x0∈R,x02-x0-1>0” |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
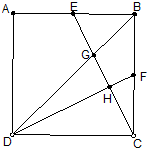 如图,已知:点E、F分别是正方形ABCD的边AB、BC的中点,BD、DF分别交CE于点G、H,若正方形ABCD的面积是240,则四边形BFHG的面积等于( )
如图,已知:点E、F分别是正方形ABCD的边AB、BC的中点,BD、DF分别交CE于点G、H,若正方形ABCD的面积是240,则四边形BFHG的面积等于( )| A. | 26 | B. | 28 | C. | 24 | D. | 30 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
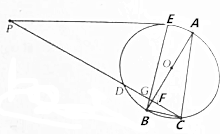 如图所示,已知圆O的一条直径为AB,PE是圆O的一条切线,E为切点,PC是圆O的一条割线,且交圆O于C,D两点,AB交PC于F,BE交PC于G,△AFC∽△ACB.
如图所示,已知圆O的一条直径为AB,PE是圆O的一条切线,E为切点,PC是圆O的一条割线,且交圆O于C,D两点,AB交PC于F,BE交PC于G,△AFC∽△ACB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com