
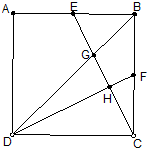
 如图,已知:点E、F分别是正方形ABCD的边AB、BC的中点,BD、DF分别交CE于点G、H,若正方形ABCD的面积是240,则四边形BFHG的面积等于( )
如图,已知:点E、F分别是正方形ABCD的边AB、BC的中点,BD、DF分别交CE于点G、H,若正方形ABCD的面积是240,则四边形BFHG的面积等于( )| A. | 26 | B. | 28 | C. | 24 | D. | 30 |
分析 要求四边形为不规则四边形,要求面积可通过其他图形的关系求解,SBFHG=S△CEB-S△BEG-S△CFH
解答 解:由题意得正方形的边长为4$\sqrt{15}$,
∴BD=4$\sqrt{30}$
∵$\frac{BE}{DC}$=$\frac{BG}{GD}$=$\frac{1}{2}$
∴BG=$\frac{4\sqrt{30}}{3}$
∴S△BEG=$\frac{1}{2}$BE×BGsin∠EBG=20
∵△CFH∽△CEB
∴$\frac{{S}_{△CFH}}{{S}_{△CEB}}$=$\frac{1}{5}$,
∴S△CFH=12,
∴SBFHC=S△CEB-S△BEG-S△CFH=28.
故选B.
点评 本题求的是不规则四边形的面积,直接求解可能比较麻烦,可通过间接法求解.


科目:高中数学 来源: 题型:选择题
| A. | y=$\frac{-1}{x}$ | B. | y=$\left\{\begin{array}{l}{\sqrt{x},x≥0}\\{\sqrt{-x},x<0}\end{array}\right.$ | C. | y=ex+e-x | D. | y=-x|x| |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
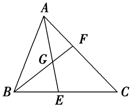 如图,△ABC中,边AC上一点F分AC为$\frac{AF}{FC}$=$\frac{2}{3}$,BF上一点G分BF为$\frac{BG}{GF}$=$\frac{3}{2}$,AG的延长线与BC交于点E,则BE:EC=3:5.
如图,△ABC中,边AC上一点F分AC为$\frac{AF}{FC}$=$\frac{2}{3}$,BF上一点G分BF为$\frac{BG}{GF}$=$\frac{3}{2}$,AG的延长线与BC交于点E,则BE:EC=3:5.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com