
分析 (1)求出导函数,利用导函数的概念求切线的斜率,点斜式写出方程即可;
(2)f(x)≥0恒成立,只需求出f(x)的最小值大于等于零即可,求出导函数,对参数a分类讨论,讨论是否满足题意;
(3)根据导函数求出函数的极小值φ(a),对极小值进行求导,利用导函数得出极小值的最大值等于零,右右不等式得证,再利用构造函数的方法,通过导函数证明左式成立.
解答 解:(1)f'(x)=4x3lnx+x3-4ax3.…(1分)
则f'(1)=1-4a.又f(1)=0,
所以,曲线y=f(x)在点(1,f(1))处的切线方程为y=(1-4a)(x-1).…(3分)
(2)由(1)得f'(x)=x3(4lnx+1-4a).
①当$a≤\frac{1}{4}$时,因为y=4lnx+1-4a为增函数,所以当x≥1时,4lnx+1-4a≥4ln1+1-4a=1-4a>0,
因此f'(x)≥0.
当且仅当$a=\frac{1}{4}$,且x=1时等号成立,
所以f(x)在(1,+∞)上为增函数.
因此,当x≥1时,f(x)≥f(1)=0.
所以,$a≤\frac{1}{4}$满足题意.…(6分)
②当$a>\frac{1}{4}$时,由f'(x)=x3(4lnx+1-4a)=0,得$lnx=a-\frac{1}{4}$,
解得$x={e^{a-\frac{1}{4}}}$.
因为$a>\frac{1}{4}$,所以$a-\frac{1}{4}>0$,所以${e^{a-\frac{1}{4}}}>{e^0}=1$.
当$x∈(1,\;{e^{a-\frac{1}{4}}})$时,f'(x)<0,因此f(x)在$(1,\;{e^{a-\frac{1}{4}}})$上为减函数.
所以当$x∈(1,\;{e^{a-\frac{1}{4}}})$时,f(x)<f(1)=0,不合题意.
综上所述,实数a的取值范围是$(-∞,\frac{1}{4}]$.…(9分)
(3)由f'(x)=x3(4lnx+1-4a)=0,得$lnx=a-\frac{1}{4}$,$x={e^{a-\frac{1}{4}}}$.
当$x∈(0,\;{e^{a-\frac{1}{4}}})$时,f'(x)<0,f(x)为减函数;当$x∈(\;{e^{a-\frac{1}{4}}},\;+∞)$时,f'(x)>0,f(x)为增函数.
所以f(x)的极小值$φ(a)=f({e^{a-\frac{1}{4}}})$=$a-\frac{1}{4}{e^{4a-1}}$.…(10分)
由φ'(a)=1-e4a-1=0,得$a=\frac{1}{4}$.
当$a∈(0,\frac{1}{4})$时,φ'(a)>0,φ(a)为增函数;当$a∈(\frac{1}{4},+∞)$时,φ'(a)<0,φ(a)为减函数.
所以$φ(a)≤φ(\frac{1}{4})=0$.…(11分)
$φ(a)-\frac{1}{4}({e^{1-\;\frac{1}{4a}}}-{e^{4a-1}})$=$a-\frac{1}{4}{e^{4a-1}}-\frac{1}{4}({e^{1-\;\frac{1}{4a}}}-{e^{4a-1}})$=$a-\frac{1}{4}{e^{1-\;\frac{1}{4a}}}$.
下证:a>0时,$a-\frac{1}{4}{e^{1-\;\frac{1}{4a}}}≥0$.
$a-\frac{1}{4}{e^{1-\;\frac{1}{4a}}}≥0$,
∴$4a≥{e^{1-\;\frac{1}{4a}}}$,
∴$ln(4a)≥1-\;\frac{1}{4a}$,
∴$ln(4a)+\frac{1}{4a}-1≥\;0$.…(12分)
令$r(a)=ln(4a)+\frac{1}{4a}-1$,则$r'(a)=\frac{1}{a}-\frac{1}{{4{a^2}}}=\frac{4a-1}{{4{a^2}}}$.
当$a∈(0,\frac{1}{4})$时,r'(a)<0,r(a)为减函数;当$a∈(\frac{1}{4},+∞)$时,r'(a)>0,r(a)为增函数.所以$r(a)≥r(\frac{1}{4})=0$,即$ln(4a)+\frac{1}{4a}-1≥\;0$.
所以$a-\frac{1}{4}{e^{1-\;\frac{1}{4a}}}≥0$,即$φ(a)-\frac{1}{4}({e^{1-\;\frac{1}{4a}}}-{e^{4a-1}})≥0$.所以$φ(a)≥\frac{1}{4}({e^{1-\;\frac{1}{4a}}}-{e^{4a-1}})$.
综上所述,要证的不等式成立.…(14分)
点评 考查了导函数的概念,恒成立问题的转化,利用导函数判断函数的最值,难点是对函数的构造,对导函数的分类讨论.


科目:高中数学 来源: 题型:填空题
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若ξ~B(4,0.25),则Dξ=1 | |
| B. | “am2<bm2”是“a<b”的充分不必要条件 | |
| C. | 若p、q均为假命题,则“p且q”为假命题 | |
| D. | 命题“?x∈R,x2-x-1≤0”的否定是“?x0∈R,x02-x0-1>0” |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
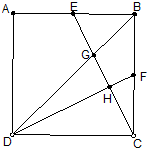 如图,已知:点E、F分别是正方形ABCD的边AB、BC的中点,BD、DF分别交CE于点G、H,若正方形ABCD的面积是240,则四边形BFHG的面积等于( )
如图,已知:点E、F分别是正方形ABCD的边AB、BC的中点,BD、DF分别交CE于点G、H,若正方形ABCD的面积是240,则四边形BFHG的面积等于( )| A. | 26 | B. | 28 | C. | 24 | D. | 30 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 购买金额 | 频数 | 频率 |
| (0,500] | 5 | 0.05 |
| (500,1000] | x | p |
| (1000,1500] | 15 | 0.15 |
| (1500,2000] | 25 | 0.25 |
| (2000,2500] | 30 | 0.3 |
| (2500,3000] | y | q |
| 合计 | 100 | 1.00 |
| 女顾客 | 男顾客 | 合计 | |
| 购物金额在2000元以上 | 35 | ||
| 购物金额在2000元以下 | 20 | ||
| 合计 | 100 |
| P(K2≥k) | 0.01 | 0.05 | 0.025 | 0.01 |
| k | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某班有25名男生、15名女生共40人,现对他们更爱好文娱还是更爱好体育进行调查,根据调查得到的数据,所绘制的二维条形图如图.
某班有25名男生、15名女生共40人,现对他们更爱好文娱还是更爱好体育进行调查,根据调查得到的数据,所绘制的二维条形图如图.| P(K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| 更爱好体育 | 更爱好文娱 | 合计 | |
| 男生 | |||
| 女生 | |||
| 合计 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com