练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    1．将方程组写成矩阵形式：
    $\left\{\begin{array}{l}{2x+y-z=0}\\{7x+10y=330}\\{5y+8z=220}\end{array}\right.$．

    分析 根据矩阵的定义即将转化成$[\begin{array}{l}{2}&{1}&{-1}\\{7}&{10}&{0}\\{0}&{5}&{8}\end{array}]$$[\begin{array}{l}{x}\\{y}\\{z}\end{array}]$=$[\begin{array}{l}{0}\\{330}\\{220}\end{array}]$．

    解答 解：将方程组转化成$[\begin{array}{l}{2}&{1}&{-1}\\{7}&{10}&{0}\\{0}&{5}&{8}\end{array}]$$[\begin{array}{l}{x}\\{y}\\{z}\end{array}]$=$[\begin{array}{l}{0}\\{330}\\{220}\end{array}]$，

    点评 本题考查矩阵与方程组的转化，考查矩阵的性质，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    5．已知直线l：x-y+2=0与圆C：x2+y2-2y-2m=0相离，则实数m的取值范围是（　　）
    A．（-∞，0）B．（-$\frac{1}{2}$，+∞）C．（-∞，-$\frac{1}{4}$）D．（-$\frac{1}{2}$，-$\frac{1}{4}$）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    6．函数f（x）=2sin（ωx+φ）（ω＞0，0＜φ＜π）的图象如图所示，已知图象经过点A（0，1），B（$\frac{π}{3}$，-1），则f（x）=$f（x）=2sin（3x+\frac{π}{6}）$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．已知函数f（x）=2+ax，若f（f（0））=4a．
    （1）求实数a的值；
    （2）计算f（3）-f（-1）的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．已知f（x）=$\frac{{{{10}^x}-{{10}^{-x}}}}{{{{10}^x}+{{10}^{-x}}}}$．
    （1）判断函数f（x）的奇偶性并证明；
    （2）证明f（x）是定义域内的增函数；
    （3）解不等式f（1-m）+f（1-m2）＞0．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．已知函数f（x）=x4lnx-a（x4-1），a∈R．
    （1）求曲线y=f（x）在点（1，f（1））处的切线方程；
    （2）若当x≥1时，f（x）≥0恒成立，求实数a的取值范围；
    （3）f（x）的极小值为φ（a），当a＞0时，求证：$\frac{1}{4}（{{e^{1-\frac{1}{4a}}}-{e^{4a-1}}}）≤φ（a）＜0$．（e=2.71828…为自然对数的底）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    13．设函数f（x）=log${\;}_{\frac{1}{2}}$（|x|）+$\frac{1}{{x}^{2}+1}$，则使得f（x）＞f（2x-1）成立的x取值范围是$（-∞，\frac{1}{3}）∪（1，+∞）$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．已知f（x）=|ax+2|，g（x）=|2x+b|．
    （1）若a=1，b=-2，求不等式f（x）-g（x）≥-2的解集；
    （2）求证：f（x）≥g（x）恒成立，的条件为ab=4且|a|≥2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

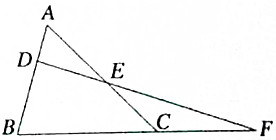    11．如图，在△ABC的边AB、AC上分别取D、E两点，使BD=CE，DE延长线交BC的延长线于F，求证：$\frac{DF}{EF}$=$\frac{AC}{AB}$．

    查看答案和解析>>

    同步练习册答案