
 函数f(x)=2sin(ωx+φ)(ω>0,0<φ<π)的图象如图所示,已知图象经过点A(0,1),B($\frac{π}{3}$,-1),则f(x)=$f(x)=2sin(3x+\frac{π}{6})$.
函数f(x)=2sin(ωx+φ)(ω>0,0<φ<π)的图象如图所示,已知图象经过点A(0,1),B($\frac{π}{3}$,-1),则f(x)=$f(x)=2sin(3x+\frac{π}{6})$. 分析 通过函数的图象求出函数的周期,然后求出ω,利用函数的图象经过的特殊点求出φ,从而可求函数解析式.
解答 解:∵图象经过点A(0,1),B($\frac{π}{3}$,-1),
A,B两个点的纵坐标相反,从点A到点B经过半个周期,
∴$\frac{π}{3}$=kT+$\frac{T}{2}$=k•$\frac{2π}{ω}$+$\frac{π}{ω}$,k∈Z,(其中T为f(x)的周期),
解得:ω=6k+3,k∈Z,
∵ω>0,
∴当k=0时,ω值为3,
又∵图象经过点A(0,1),f(x)=2sin(ωx+φ),
∴1=2sinφ,即sinφ=$\frac{1}{2}$,
∴由0<φ<π,由函数的图象可得φ=$\frac{π}{6}$,
∴$f(x)=2sin(3x+\frac{π}{6})$.
故答案为:$f(x)=2sin(3x+\frac{π}{6})$.
点评 本题主要考查了由y=Asin(ωx+φ)的部分图象确定其解析式,考查了三角函数的图象的应用,周期的求法,函数的图象经过的特殊点的应用,考查计算能力,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{1}{2}$,$\frac{1}{2}$] | B. | [-$\frac{1}{2}$,0] | C. | [0,$\sqrt{6}$] | D. | [0,$\frac{1}{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
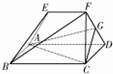 多面体ABCDFE中,底面四边形ABCD为矩形,EF∥AD,AE=FD,FG=GD,AD=2AB=2EF=2,且四边形EADF的面积为$\frac{3\sqrt{3}}{4}$.
多面体ABCDFE中,底面四边形ABCD为矩形,EF∥AD,AE=FD,FG=GD,AD=2AB=2EF=2,且四边形EADF的面积为$\frac{3\sqrt{3}}{4}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
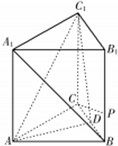 正三棱柱ABC-A1B1C1中,AB=6,AA1=4,D为BC的中点.
正三棱柱ABC-A1B1C1中,AB=6,AA1=4,D为BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若ξ~B(4,0.25),则Dξ=1 | |
| B. | “am2<bm2”是“a<b”的充分不必要条件 | |
| C. | 若p、q均为假命题,则“p且q”为假命题 | |
| D. | 命题“?x∈R,x2-x-1≤0”的否定是“?x0∈R,x02-x0-1>0” |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,△ABC为⊙O的内接三角形,D,E分别为BC,AB的中点,直线DE交圆O于F,G,且直线DE与过A点的切线交于点P,DF=1,DE=2,PE=3.
如图,△ABC为⊙O的内接三角形,D,E分别为BC,AB的中点,直线DE交圆O于F,G,且直线DE与过A点的切线交于点P,DF=1,DE=2,PE=3.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com