
 如图,△ABC为⊙O的内接三角形,D,E分别为BC,AB的中点,直线DE交圆O于F,G,且直线DE与过A点的切线交于点P,DF=1,DE=2,PE=3.
如图,△ABC为⊙O的内接三角形,D,E分别为BC,AB的中点,直线DE交圆O于F,G,且直线DE与过A点的切线交于点P,DF=1,DE=2,PE=3.分析 (1)证明两组对应角相等,即可证明:△PEA~△BDE;
(2)设PG=y,GE=x,则x+y=3,利用三角形相似,可得$\frac{\sqrt{3x}}{\sqrt{2+x}}$=$\frac{3}{\sqrt{6y}}$,由此求线段PA的长.
解答 (1)证明:∵PA是过点A的切线,
∴∠BAP=∠BCA.
∵DE∥AC,
∴∠BCA=∠BDE,
∵∠BEA=∠PEA,
∴△PEA~△BDE;
(2)设PG=y,GE=x,则x+y=3①,
PA=$\sqrt{6y}$,BD=$\sqrt{2+x}$,BE=$\sqrt{3x}$,
∵△PEA~△BDE,
∴$\frac{EB}{BD}$=$\frac{PE}{AP}$,
∴$\frac{\sqrt{3x}}{\sqrt{2+x}}$=$\frac{3}{\sqrt{6y}}$②,
由①②可得x=2,y=1或x=$\frac{1}{2}$,y=$\frac{5}{2}$,
∴PA=$\sqrt{6}$或PA=$\sqrt{15}$.
点评 本题考查三角形相似的判定与性质,考查学生分析解决问题的能力,考查学生的计算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
 函数f(x)=2sin(ωx+φ)(ω>0,0<φ<π)的图象如图所示,已知图象经过点A(0,1),B($\frac{π}{3}$,-1),则f(x)=$f(x)=2sin(3x+\frac{π}{6})$.
函数f(x)=2sin(ωx+φ)(ω>0,0<φ<π)的图象如图所示,已知图象经过点A(0,1),B($\frac{π}{3}$,-1),则f(x)=$f(x)=2sin(3x+\frac{π}{6})$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 男 | 女 | 总计 | |
| 需要帮助 | 40 | m | 70 |
| 不需要帮助 | n | 270 | s |
| 总计 | 200 | t | 500 |
| y1 | y2 | 总计 | |
| x1 | a | b | a+b |
| x2 | c | d | c+d |
| 总计 | a+c | b+d | a+b+c+d |
| P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
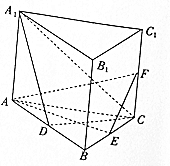 如图,直三棱柱ABC-A1B1C1的底面为正三角形,E、F分别是BC、CC1的中点.
如图,直三棱柱ABC-A1B1C1的底面为正三角形,E、F分别是BC、CC1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
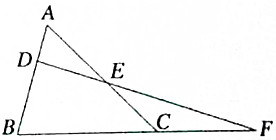 如图,在△ABC的边AB、AC上分别取D、E两点,使BD=CE,DE延长线交BC的延长线于F,求证:$\frac{DF}{EF}$=$\frac{AC}{AB}$.
如图,在△ABC的边AB、AC上分别取D、E两点,使BD=CE,DE延长线交BC的延长线于F,求证:$\frac{DF}{EF}$=$\frac{AC}{AB}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
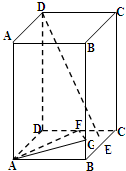 如图,在正四棱柱ABCD-A1B1C1D1中,侧棱AA1=2AB,E是BC中点,F是CD中点,
如图,在正四棱柱ABCD-A1B1C1D1中,侧棱AA1=2AB,E是BC中点,F是CD中点,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com