
分析 (1)若a=1,b=-2,分类讨论求不等式f(x)-g(x)≥-2的解集;
(2)f(x)≥g(x),即|ax+2|≥|2x+b|,即(a2-4)x2+(4a-4b)x+4-b2≥0,利用二次函数的性质,即可证明结论.
解答 (1)解:a=1,b=-2,不等式f(x)-g(x)≥-2,即|x+2|-|2x-2|≥-2.
x≤-2时,-x-2+2x-2≥-2,解得x≥2,无解;
-2<x<1时,x+2+2x-2≥-2,解得x≥-$\frac{2}{3}$,∴-$\frac{2}{3}$≤x<1;
x≥1时,x+2-2x+2≥-2,解得x≤6,∴1≤x≤6;
综上所述,不等式的解集为{x|-$\frac{2}{3}$≤x≤6};
(2)证明:f(x)≥g(x),即|ax+2|≥|2x+b|.
∴(a2-4)x2+(4a-4b)x+4-b2≥0,
∵f(x)≥g(x)恒成立,
∴$\left\{\begin{array}{l}{{a}^{2}-4≥0}\\{(4a-4b)^{2}-4({a}^{2}-4)(4-{b}^{2})≤0}\end{array}\right.$,
∴$\left\{\begin{array}{l}{|a|≥2}\\{(ab-4)^{2}≤0}\end{array}\right.$,
∴ab=4且|a|≥2.
点评 本题考查绝对值不等式的解法,考查恒成立问题,考查分类讨论的数学思想,属于中档题.


 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:高中数学 来源: 题型:解答题
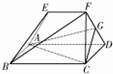 多面体ABCDFE中,底面四边形ABCD为矩形,EF∥AD,AE=FD,FG=GD,AD=2AB=2EF=2,且四边形EADF的面积为$\frac{3\sqrt{3}}{4}$.
多面体ABCDFE中,底面四边形ABCD为矩形,EF∥AD,AE=FD,FG=GD,AD=2AB=2EF=2,且四边形EADF的面积为$\frac{3\sqrt{3}}{4}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 购买金额 | 频数 | 频率 |
| (0,500] | 5 | 0.05 |
| (500,1000] | x | p |
| (1000,1500] | 15 | 0.15 |
| (1500,2000] | 25 | 0.25 |
| (2000,2500] | 30 | 0.3 |
| (2500,3000] | y | q |
| 合计 | 100 | 1.00 |
| 女顾客 | 男顾客 | 合计 | |
| 购物金额在2000元以上 | 35 | ||
| 购物金额在2000元以下 | 20 | ||
| 合计 | 100 |
| P(K2≥k) | 0.01 | 0.05 | 0.025 | 0.01 |
| k | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a为任意实数 | B. | a=f′(3) | C. | a>f′(3) | D. | a<f′(3) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某班有25名男生、15名女生共40人,现对他们更爱好文娱还是更爱好体育进行调查,根据调查得到的数据,所绘制的二维条形图如图.
某班有25名男生、15名女生共40人,现对他们更爱好文娱还是更爱好体育进行调查,根据调查得到的数据,所绘制的二维条形图如图.| P(K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| 更爱好体育 | 更爱好文娱 | 合计 | |
| 男生 | |||
| 女生 | |||
| 合计 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,△ABC为⊙O的内接三角形,D,E分别为BC,AB的中点,直线DE交圆O于F,G,且直线DE与过A点的切线交于点P,DF=1,DE=2,PE=3.
如图,△ABC为⊙O的内接三角形,D,E分别为BC,AB的中点,直线DE交圆O于F,G,且直线DE与过A点的切线交于点P,DF=1,DE=2,PE=3.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 优秀 | 非优秀 | 总计 | |
| 甲班 | 10 | ||
| 乙班 | 30 | ||
| 合计 | 100 |
| p(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com