
| 优秀 | 非优秀 | 总计 | |
| 甲班 | 10 | ||
| 乙班 | 30 | ||
| 合计 | 100 |
| p(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
分析 (1)数学考试优秀人数有100×$\frac{3}{10}$=30人,即可将2×2列联表补充完整;
(2)根据2×2列联表,代入求临界值的公式,求出观测值,利用观测值同临界值表进行比较,由K2≈4.762>3.841,故有95%的把握认为“成绩与班级有关系”;
(3)根据分层抽样甲班2人,乙班4人,则甲班被抽到的人数为ξ的取值0,1,2,分别求得其概率及分布列,根据分布列求得其数学期望.
解答 解:(1)数学考试优秀人数有100×$\frac{3}{10}$=30人 …(1分)
补充完成2×2列联表如下:…(3分)
| 优秀 | 非优秀 | 总计 | |
| 甲班 | 10 | 40 | 50 |
| 乙班 | 20 | 30 | 50 |
| 合计 | 30 | 70 | 100 |
| ξ | 0 | 1 | 2 |
| P | $\frac{2}{5}$ | $\frac{8}{15}$ | $\frac{1}{15}$ |
点评 本题考查独立性检验知识的运用,考查超几何分布的概率计算公式、分布列及数学期望,考查计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
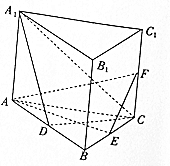 如图,直三棱柱ABC-A1B1C1的底面为正三角形,E、F分别是BC、CC1的中点.
如图,直三棱柱ABC-A1B1C1的底面为正三角形,E、F分别是BC、CC1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
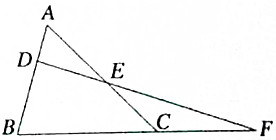 如图,在△ABC的边AB、AC上分别取D、E两点,使BD=CE,DE延长线交BC的延长线于F,求证:$\frac{DF}{EF}$=$\frac{AC}{AB}$.
如图,在△ABC的边AB、AC上分别取D、E两点,使BD=CE,DE延长线交BC的延长线于F,求证:$\frac{DF}{EF}$=$\frac{AC}{AB}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com