
分析 由题意画出图形,设出棱锥的底面边长,找出棱锥外接球的球心,然后通过分类求解直角三角形得答案.
解答 解:如图,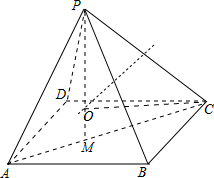
由题意可知,四棱锥P-ABCD是正四棱锥,过P作PM⊥平面ABCD,垂足为M,
则M是底面正方形的中心,设底面边长为a,则AC=$\sqrt{2}a$,MC=$\frac{\sqrt{2}}{2}a$,
作PC的垂直平分线角PM于O,∴O为四棱锥外接球的球心,连接OC,
在Rt△PMC中,∵PC=$\sqrt{3}$,MC=$\frac{\sqrt{2}}{2}a$,∴PM=$\sqrt{3-\frac{1}{2}{a}^{2}}$,
在Rt△PMC中,∵OC=2,MC=$\frac{\sqrt{2}}{2}a$,∴OM=$\sqrt{4-\frac{1}{2}{a}^{2}}$,
则$\sqrt{3-\frac{1}{2}{a}^{2}}=2-\sqrt{4-\frac{1}{2}{a}^{2}}$①,或$\sqrt{3-\frac{1}{2}{a}^{2}}=2+\sqrt{4-\frac{1}{2}{a}^{2}}$②,
解①得:${a}^{2}=\frac{39}{8}$,代入PM=$\sqrt{3-\frac{1}{2}{a}^{2}}$,得PM=$\frac{3}{4}$;解②得:a不存在.
∴四棱锥P-ABCD的高为$\frac{3}{4}$.
故答案为:$\frac{3}{4}$.
点评 本题考查棱锥的结构特征,考查空间想象能力和运算能力,是中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
 某班有25名男生、15名女生共40人,现对他们更爱好文娱还是更爱好体育进行调查,根据调查得到的数据,所绘制的二维条形图如图.
某班有25名男生、15名女生共40人,现对他们更爱好文娱还是更爱好体育进行调查,根据调查得到的数据,所绘制的二维条形图如图.| P(K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| 更爱好体育 | 更爱好文娱 | 合计 | |
| 男生 | |||
| 女生 | |||
| 合计 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
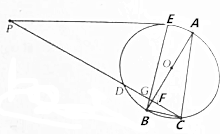 如图所示,已知圆O的一条直径为AB,PE是圆O的一条切线,E为切点,PC是圆O的一条割线,且交圆O于C,D两点,AB交PC于F,BE交PC于G,△AFC∽△ACB.
如图所示,已知圆O的一条直径为AB,PE是圆O的一条切线,E为切点,PC是圆O的一条割线,且交圆O于C,D两点,AB交PC于F,BE交PC于G,△AFC∽△ACB.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 优秀 | 非优秀 | 总计 | |
| 甲班 | 10 | ||
| 乙班 | 30 | ||
| 合计 | 100 |
| p(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
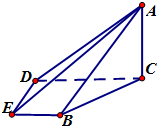 如图,在四棱锥A-BCDE中,平面ABC⊥平面BCDE,∠CDE=∠BED=90°,AB=CD=2,DE=BE=1,AC=$\sqrt{2}$.
如图,在四棱锥A-BCDE中,平面ABC⊥平面BCDE,∠CDE=∠BED=90°,AB=CD=2,DE=BE=1,AC=$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com