
 某班有25名男生、15名女生共40人,现对他们更爱好文娱还是更爱好体育进行调查,根据调查得到的数据,所绘制的二维条形图如图.
某班有25名男生、15名女生共40人,现对他们更爱好文娱还是更爱好体育进行调查,根据调查得到的数据,所绘制的二维条形图如图.| P(K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| 更爱好体育 | 更爱好文娱 | 合计 | |
| 男生 | |||
| 女生 | |||
| 合计 |
分析 (1)根据图中数据,作出2×2列联表,代入求临界值的公式,求出观测值,利用观测值同临界值表进行比较,K2≈2,667<2.706.不能在犯错概率不超过0.10的前提下认为性别与更爱好体育有关系;
(2)选2人中女生人数X取值为0,1,2,分别求得P(X=0),P(X=1),P(X=2),完成分布列表格,即可求得2人中女生人数X的期望E(X);
(3)由题意知是一个等可能事件的概率,试验发生包含的事件数是20×20,满足条件的事件是一男一女,共有15×10+5×10,得到概率.
解答 解:(1)将二维条形转化成2×2列联表:
| 更爱好体育 | 更爱好文娱 | 合计 | |
| 男生 | 15 | 10 | 25 |
| 女生 | 5 | 10 | 15 |
| 合计 | 20 | 20 | 40 |
| X | 0 | 1 | 2 |
| P | $\frac{21}{38}$ | $\frac{5}{38}$ | $\frac{1}{19}$ |
点评 本题考查独立性检验知识的运用,考查超几何分布的计算公式、分布列和数学期望及其排列与组合的计算公式,考查计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
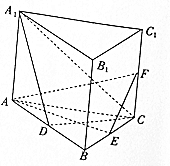 如图,直三棱柱ABC-A1B1C1的底面为正三角形,E、F分别是BC、CC1的中点.
如图,直三棱柱ABC-A1B1C1的底面为正三角形,E、F分别是BC、CC1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com