
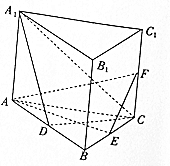
 如图,直三棱柱ABC-A1B1C1的底面为正三角形,E、F分别是BC、CC1的中点.
如图,直三棱柱ABC-A1B1C1的底面为正三角形,E、F分别是BC、CC1的中点.分析 (1)由B1B⊥平面ABC,可得B1B⊥AE,利用△ABC是等边三角形,可得AE⊥BC,可得AE⊥平面BCC1B1,即可证明平面AEF⊥平面B1BCC1.
(2)由(1)可知CD⊥平面ABB1A1,CD⊥A1D,再利用等边三角形的性质、勾股定理可得AA1,FC.利用直角三角形的面积计算公式即可得出.
解答 (1)证明:∵B1B⊥平面ABC,AE?平面ABC,
∴B1B⊥AE,
∵△ABC是等边三角形,E是BC的中点,
∴AE⊥BC,又BC?平面BCC1B1,B1B?平面BCC1B1,B1B∩BC=B,
∴AE⊥平面BCC1B1,又AE?平面AEF,
∴平面AEF⊥平面B1BCC1.
(2)解:由(1)可知CD⊥平面ABB1A1,A1D?平面ABB1A1,
∴CD⊥A1D,
∵AB=AC=BC=2,D是AB的中点,E是BC的中点,
∴AE=CD=$\sqrt{3}$,AD=CE=1,
∵∠CA1D=45°,∴A1D=CD=$\sqrt{3}$,
∴AA1=$\sqrt{{A}_{1}{D}^{2}-A{D}^{2}}$=$\sqrt{2}$,
∵F是C1C的中点,FC=$\frac{1}{2}A{A}_{1}$=$\frac{\sqrt{2}}{2}$.
∴三棱锥F-AEC的表面积S=$\frac{1}{2}×1×\frac{\sqrt{2}}{2}$+$\frac{1}{2}×2×\frac{\sqrt{2}}{2}$+$\frac{1}{2}×1×\sqrt{3}$+$\frac{1}{2}×\sqrt{3}×\sqrt{(\frac{\sqrt{2}}{2})^{2}+1}$=$\frac{3\sqrt{2}+\sqrt{3}}{2}$.
点评 本题考查了空间位置关系、等边三角形的性质、直角三角形的面积计算公式、勾股定理,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 若ξ~B(4,0.25),则Dξ=1 | |
| B. | “am2<bm2”是“a<b”的充分不必要条件 | |
| C. | 若p、q均为假命题,则“p且q”为假命题 | |
| D. | 命题“?x∈R,x2-x-1≤0”的否定是“?x0∈R,x02-x0-1>0” |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 购买金额 | 频数 | 频率 |
| (0,500] | 5 | 0.05 |
| (500,1000] | x | p |
| (1000,1500] | 15 | 0.15 |
| (1500,2000] | 25 | 0.25 |
| (2000,2500] | 30 | 0.3 |
| (2500,3000] | y | q |
| 合计 | 100 | 1.00 |
| 女顾客 | 男顾客 | 合计 | |
| 购物金额在2000元以上 | 35 | ||
| 购物金额在2000元以下 | 20 | ||
| 合计 | 100 |
| P(K2≥k) | 0.01 | 0.05 | 0.025 | 0.01 |
| k | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某班有25名男生、15名女生共40人,现对他们更爱好文娱还是更爱好体育进行调查,根据调查得到的数据,所绘制的二维条形图如图.
某班有25名男生、15名女生共40人,现对他们更爱好文娱还是更爱好体育进行调查,根据调查得到的数据,所绘制的二维条形图如图.| P(K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| 更爱好体育 | 更爱好文娱 | 合计 | |
| 男生 | |||
| 女生 | |||
| 合计 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,△ABC为⊙O的内接三角形,D,E分别为BC,AB的中点,直线DE交圆O于F,G,且直线DE与过A点的切线交于点P,DF=1,DE=2,PE=3.
如图,△ABC为⊙O的内接三角形,D,E分别为BC,AB的中点,直线DE交圆O于F,G,且直线DE与过A点的切线交于点P,DF=1,DE=2,PE=3.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
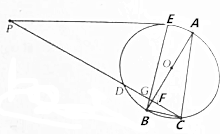 如图所示,已知圆O的一条直径为AB,PE是圆O的一条切线,E为切点,PC是圆O的一条割线,且交圆O于C,D两点,AB交PC于F,BE交PC于G,△AFC∽△ACB.
如图所示,已知圆O的一条直径为AB,PE是圆O的一条切线,E为切点,PC是圆O的一条割线,且交圆O于C,D两点,AB交PC于F,BE交PC于G,△AFC∽△ACB.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 优秀 | 非优秀 | 总计 | |
| 甲班 | 10 | ||
| 乙班 | 30 | ||
| 合计 | 100 |
| p(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com