
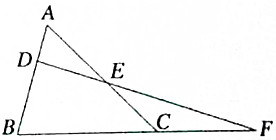
 如图,在△ABC的边AB、AC上分别取D、E两点,使BD=CE,DE延长线交BC的延长线于F,求证:$\frac{DF}{EF}$=$\frac{AC}{AB}$.
如图,在△ABC的边AB、AC上分别取D、E两点,使BD=CE,DE延长线交BC的延长线于F,求证:$\frac{DF}{EF}$=$\frac{AC}{AB}$. 科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,△ABC为⊙O的内接三角形,D,E分别为BC,AB的中点,直线DE交圆O于F,G,且直线DE与过A点的切线交于点P,DF=1,DE=2,PE=3.
如图,△ABC为⊙O的内接三角形,D,E分别为BC,AB的中点,直线DE交圆O于F,G,且直线DE与过A点的切线交于点P,DF=1,DE=2,PE=3.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 优秀 | 非优秀 | 总计 | |
| 甲班 | 10 | ||
| 乙班 | 30 | ||
| 合计 | 100 |
| p(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 成功(人) | 失败(人) | 合计 | |
| 20~30(岁) | 20 | 40 | 60 |
| 30~40(岁) | 50 | ||
| 合计 | 70 |
| P(K2≥k) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源:2017届甘肃会宁县一中高三上学期9月月考数学(文)试卷(解析版) 题型:解答题
已知函数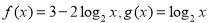 .
.
(1)当x∈[1,4]时,求函数 的值域;
的值域;
(2)如果对任意的x∈[1,4],不等式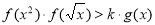 恒成立,求实数k的取值范围
恒成立,求实数k的取值范围
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com