
| 成功(人) | 失败(人) | 合计 | |
| 20~30(岁) | 20 | 40 | 60 |
| 30~40(岁) | 50 | ||
| 合计 | 70 |
| P(K2≥k) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
分析 (1)由已知条件求得根据30~40岁年龄段的总人数,再根据表格数据,即可完成2×2列联表;
(2)根据2×2列联表,代入求临界值的公式,求出观测值,利用观测值同临界值表进行比较,K2≈7.14>6.635,有99%的把握认为闯关成功与年龄有关
解答 解:(1)由30~40岁年龄段中随机选取一人,其恰好闯关成功的概率为$\frac{5}{9}$,
30~40岁年龄段的总人数为$\frac{50}{\frac{5}{9}}$=90,
即可完成2×2列联表:
| 成功(人) | 失败(人) | 合计 | |
| 20~30(岁) | 20 | 40 | 60 |
| 30~40(岁) | 50 | 40 | 90 |
| 合计 | 70 | 80 | 150 |
点评 本题考查独立性检验的应用,考查学生的计算能力,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 男 | 女 | 总计 | |
| 需要帮助 | 40 | m | 70 |
| 不需要帮助 | n | 270 | s |
| 总计 | 200 | t | 500 |
| y1 | y2 | 总计 | |
| x1 | a | b | a+b |
| x2 | c | d | c+d |
| 总计 | a+c | b+d | a+b+c+d |
| P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
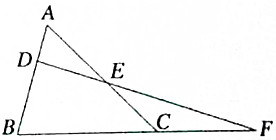 如图,在△ABC的边AB、AC上分别取D、E两点,使BD=CE,DE延长线交BC的延长线于F,求证:$\frac{DF}{EF}$=$\frac{AC}{AB}$.
如图,在△ABC的边AB、AC上分别取D、E两点,使BD=CE,DE延长线交BC的延长线于F,求证:$\frac{DF}{EF}$=$\frac{AC}{AB}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,平行四边形ABCD中,AE:EB=1:2.
如图,平行四边形ABCD中,AE:EB=1:2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com