
分析 (1)利用函数的奇偶性的定义判断证明f(-x)=-$\frac{{{{10}^x}-{{10}^{-x}}}}{{{{10}^x}+{{10}^{-x}}}}$=-f(x),即可判定函数的奇偶性;
(2)利用函数单调性的定义,设x1<x2,利用作差法证明f(x1)<f(x2),即可得出函数的单调性;
(3)根据函数的单调性与奇偶性,化抽象函数为具体函数,即可解不等式.
解答 解(1)(x)是奇函数,理由如下:
∵f(x)的定义域为R,且f(-x)=-$\frac{{{{10}^x}-{{10}^{-x}}}}{{{{10}^x}+{{10}^{-x}}}}$=-f(x),
∴f(x)是奇函数.…(4分)
证明:(2)f(x)=$\frac{{{{10}^x}-{{10}^{-x}}}}{{{{10}^x}+{{10}^{-x}}}}$=1-$\frac{2}{1{0}^{2x}+1}$
设x1<x2,则 …(5分)
f(x1)-f(x2)=1-$\frac{2}{1{0}^{2{x}_{1}}+1}$--(1-$\frac{2}{1{0}^{2{x}_{2}}+1}$)=$\frac{2(1{0}^{2{x}_{1}}-1{0}^{2{x}_{2}})}{(1{0}^{2{x}_{1}}+1)(1{0}^{2{x}_{2}}+1)}$ …(7分)
∵y=10x为增函数,
∴当x1<x2时,$1{0}^{2{x}_{1}}-1{0}^{2{x}_{2}}$<0,
∴f(x1)-f(x2)<0,即f(x1)<f(x2).
∴f(x)在定义域上为增函数.…(9分)
(3)不等式可化为f(1-m)>-f(1-m2) …(10分)
由(1)知f(x)是奇函数,
∴f(1-m)>f(m2-1)…(11分)
由(2)知f(x)在定义域上为增函数,
∴1-m>m2-1 …(12分)
解得-2<m<1.…(14分)
点评 本题考查函数的奇偶性与单调性,考查学生解不等式的能力,正确转化是关键.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
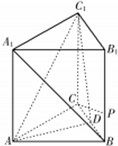 正三棱柱ABC-A1B1C1中,AB=6,AA1=4,D为BC的中点.
正三棱柱ABC-A1B1C1中,AB=6,AA1=4,D为BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 0 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a为任意实数 | B. | a=f′(3) | C. | a>f′(3) | D. | a<f′(3) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 成功(人) | 失败(人) | 合计 | |
| 20~30(岁) | 20 | 40 | 60 |
| 30~40(岁) | 50 | ||
| 合计 | 70 |
| P(K2≥k) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com