
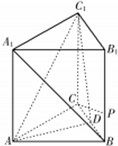
 正三棱柱ABC-A1B1C1中,AB=6,AA1=4,D为BC的中点.
正三棱柱ABC-A1B1C1中,AB=6,AA1=4,D为BC的中点.分析 (1)连接A1C交AC1于E,连结DE,利用中位线定理可得DE∥A1B,于是A1B∥平面AC1D;
(2)假设CP⊥C1D于F,利用△PCB∽△DCF∽△DC1C,利用比例式即可得出BP的长;
(3)证明AD⊥平面BCC1B1可得AD⊥C1D,利用V${\;}_{C-AD{C}_{1}}$=V${\;}_{{C}_{1}-ACD}$计算点C到平面ADC1的距离.
解答 解:(1)连接A1C交AC1于E,连结DE,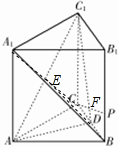
∵四边形ACC1A1是矩形,
∴E为A1C的中点,又D为BC的中点,
∴DE∥A1B,
又DE?平面AC1D,A1B?AC1D,
∴A1B∥平面AC1D.
(2)假设存在点P使得CP⊥平面ADC1,设CP与C1D交于F,
∵C1D?平面ADC1,
∴CP⊥C1D,
∵BB1⊥BC,∠DCF=∠PCB,
∴△DCF∽△PCB,
又△C1CD∽△CFD,
∴△C1CD∽△CBP,
∴$\frac{C{C}_{1}}{BC}=\frac{CD}{BP}$,即$\frac{4}{6}=\frac{3}{BP}$,
解得BP=$\frac{9}{2}$>4,
∴线段BB1不存在点P使得CP⊥平面ADC1.
(3)∵△ABC是等边三角形,D是BC的中点,AB=6,
∴AD⊥BC,AD=3$\sqrt{3}$,
∵BB1⊥平面ABC,AD?平面ABC,
∴BB1⊥AD,又BC∩BB1=B,
∴AD⊥平面BB1C1C,
∴AD⊥C1D,
∵C1D=$\sqrt{C{{C}_{1}}^{2}+C{D}^{2}}$=5,∴S${\;}_{△A{C}_{1}D}$=$\frac{1}{2}AD•{C}_{1}D$=$\frac{15\sqrt{3}}{2}$,
设C到平面ADC1的距离为h,则V${\;}_{C-AD{C}_{1}}$=$\frac{1}{3}{S}_{△A{C}_{1}D}•h$=$\frac{5\sqrt{3}}{2}h$,
∵S△ACD=$\frac{1}{2}AD•CD$=$\frac{9\sqrt{3}}{2}$,∴V${\;}_{{C}_{1}-ACD}$=$\frac{1}{3}{S}_{△ACD}•C{C}_{1}$=6$\sqrt{3}$,
∵V${\;}_{C-AD{C}_{1}}$=V${\;}_{{C}_{1}-ACD}$,∴$\frac{5\sqrt{3}}{2}h=6\sqrt{3}$,
∴h=$\frac{12}{5}$.
∴点C到平面ADC1的距离为$\frac{12}{5}$.
点评 本题考查了线面平行的判定与性质,点到平面的距离计算,属于中档题.


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:高中数学 来源: 题型:解答题
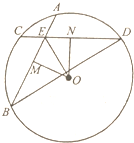 如图,在圆O中,相交于点E的两弦AB,CD的中点分别为M,N.
如图,在圆O中,相交于点E的两弦AB,CD的中点分别为M,N.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
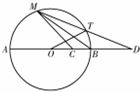 如图所示,直线DA过圆O的圆心,且交圆O于A,B两点,BC=CO=$\frac{1}{2}$BD,DM为圆O的一条割线,且与圆O交于M,T两点.
如图所示,直线DA过圆O的圆心,且交圆O于A,B两点,BC=CO=$\frac{1}{2}$BD,DM为圆O的一条割线,且与圆O交于M,T两点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 函数f(x)=2sin(ωx+φ)(ω>0,0<φ<π)的图象如图所示,已知图象经过点A(0,1),B($\frac{π}{3}$,-1),则f(x)=$f(x)=2sin(3x+\frac{π}{6})$.
函数f(x)=2sin(ωx+φ)(ω>0,0<φ<π)的图象如图所示,已知图象经过点A(0,1),B($\frac{π}{3}$,-1),则f(x)=$f(x)=2sin(3x+\frac{π}{6})$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1] | B. | [0,1] | C. | [1,+∞) | D. | (-∞,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 男 | 女 | 总计 | |
| 需要帮助 | 40 | m | 70 |
| 不需要帮助 | n | 270 | s |
| 总计 | 200 | t | 500 |
| y1 | y2 | 总计 | |
| x1 | a | b | a+b |
| x2 | c | d | c+d |
| 总计 | a+c | b+d | a+b+c+d |
| P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com