
分析 (Ⅰ)方法一:利用点A(2,$\sqrt{2}$)在椭圆C上,且AF2与x轴垂直.求出a,c然后求出b,即可求解椭圆C的方程.
方法二:利用已知条件,椭圆的定义,求解a,b,然后求解椭圆C的方程.
(Ⅱ)设B(x2,y2)由题意知直线AB的斜率必存在,设为k,得到直线AB的方程为$y-\sqrt{2}=k(x-2)$,代入椭圆C的方程,利用△>0恒成立,以及韦达定理,求解弦长|AB|,求出点O到直线AB的距离,表示三角形的面积,然后求解直线的斜率.
解答 (本小题满分12分)
解:(Ⅰ)方法一:$c=2,\frac{b^2}{a}=\sqrt{2}$,
∴${b^2}=\sqrt{2}a={a^2}-4∴{a^2}-\sqrt{2}a-4=0$
解得$a=2\sqrt{2}$或$a=-\sqrt{2}$(舍)
∴b=2
∴椭圆C的方程为$\frac{x^2}{8}+\frac{y^2}{4}=1$
方法二:$|{A{F_2}}|=\sqrt{2},|{{F_1}{F_2}}|=2C=4,Rt△A{F_2}{F_1}$中,
$|{A{F_1}}|=3\sqrt{2}∴2a=|{A{F_1}}|+|{A{F_2}}|=4\sqrt{2}$∴$a=2\sqrt{2}$
∴b=2∴椭圆C的方程为$\frac{x^2}{8}+\frac{y^2}{4}=1$…(4分)
(Ⅱ)设B(x2,y2)由题意知直线AB的斜率必存在,设为k,
则直线AB的方程为$y-\sqrt{2}=k(x-2)$代入椭圆C的方程$\frac{x^2}{8}+\frac{y^2}{4}=1$
得$({1+2{k^2}}){x^2}-(8{k^2}-4\sqrt{2}k)x+8{k^2}-8\sqrt{2}k-4=0$,
△>0恒成立,${x_1}{x_2}=\frac{{8{k^2}-8\sqrt{2}k-4}}{{1+2{k^2}}},{x_1}=2$,
∴${x_2}=\frac{{4{k^2}-4\sqrt{2}k-2}}{{1+2{k^2}}}$…(6分)
∴$|{AB}|=\sqrt{(1+{k^2}){{({x_1}-{x_2})}^2}}=\sqrt{(1+{k^2}){{(\frac{{4\sqrt{2}k+4}}{{1+2{k^2}}})}^2}}$,
点O到直线AB的距离为$d=\frac{{|{\sqrt{2}-2k}|}}{{\sqrt{1+{k^2}}}}$.
∴${S_{△AOB}}=\frac{1}{2}|{AB}|•d=\frac{1}{2}•$$\frac{{|{\sqrt{2}-2k}|}}{{\sqrt{1+{k^2}}}}•$$\sqrt{(1+{k^2}){{(\frac{{4\sqrt{2}k+4}}{{1+2{k^2}}})}^2}}$=$\frac{{2\sqrt{2}|{2{k^2}-1}|}}{{1+2{k^2}}}=\frac{{2\sqrt{2}}}{3}$…(9分)
∴3|2k2-1|=1+2k2∴k2=1或${k^2}=\frac{1}{4}$,
∴k=1或k=-1或$k=\frac{1}{2}$或$k=-\frac{1}{2}$.…(12分)
点评 本题考查椭圆的方程的求法,椭圆的定义的应用,直线与椭圆的位置关系的综合应用,弦长公式以及设而不求思想的应用,考查转化思想以及计算能力.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:解答题
 广播电台为了了解某地区的听众对某个戏曲节目的收听情况,随机抽取了100名听众进行调查,下面是根据调查结果绘制的听众日均收听该节目的频率分布直方图,将日均收听该节目时间不低于40分钟的听众成为“戏迷”
广播电台为了了解某地区的听众对某个戏曲节目的收听情况,随机抽取了100名听众进行调查,下面是根据调查结果绘制的听众日均收听该节目的频率分布直方图,将日均收听该节目时间不低于40分钟的听众成为“戏迷”| “戏迷” | 非戏迷 | 总计 | |
| 男 | |||
| 女 | 10 | 55 | |
| 总计 |
| P(K2≥k) | 0.05 | 0.01 |
| k | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 三条两两相交的直线一定在同一面内 | |
| B. | 垂直于同一条直线的两条直线一定平行 | |
| C. | m,n是平面α内的两条相交直线,l1,l2是平面β内的两条相交直线,若m∥l1,n∥l2,则α∥β | |
| D. | α,β,η是三个不同的平面,若α⊥η,β⊥η,则α∥β |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 210 | B. | 420 | C. | 630 | D. | 840 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
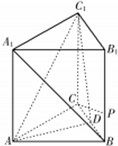 正三棱柱ABC-A1B1C1中,AB=6,AA1=4,D为BC的中点.
正三棱柱ABC-A1B1C1中,AB=6,AA1=4,D为BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com