
 广播电台为了了解某地区的听众对某个戏曲节目的收听情况,随机抽取了100名听众进行调查,下面是根据调查结果绘制的听众日均收听该节目的频率分布直方图,将日均收听该节目时间不低于40分钟的听众成为“戏迷”
广播电台为了了解某地区的听众对某个戏曲节目的收听情况,随机抽取了100名听众进行调查,下面是根据调查结果绘制的听众日均收听该节目的频率分布直方图,将日均收听该节目时间不低于40分钟的听众成为“戏迷”| “戏迷” | 非戏迷 | 总计 | |
| 男 | |||
| 女 | 10 | 55 | |
| 总计 |
| P(K2≥k) | 0.05 | 0.01 |
| k | 3.841 | 6.635 |
分析 (Ⅰ)由频率分布直方图求得“戏迷”有25人,完成2×2列联表,根据2×2列联表,代入求临界值的公式,求出观测值,利用观测值同临界值表进行比较,K2≈3.030<3.841,故没有理由认为“戏迷”与性别有关;
(Ⅱ)由题意可知X~B(3,$\frac{1}{4}$),根据二项分布求得其分布列,数学期望及方差.
解答 解:(Ⅰ)由频率分布直方图可知在抽取的100人中,“戏迷”有(0.02+0.005)×10×100=25人,
“戏迷”有25人,-----(1分)
2×2列联表如下:
| “戏迷” | 非戏迷 | 总计 | |
| 男 | 15 | 30 | 45 |
| 女 | 10 | 45 | 55 |
| 总计 | 25 | 75 | 100 |
| X | 0 | 1 | 2 | 3 |
| P | $\frac{27}{64}$ | $\frac{27}{64}$ | $\frac{9}{64}$ | $\frac{1}{64}$ |
点评 本题考查独立性检验知识的运用,考查二项分布的计算公式、分布列和数学期望及方差的计算公式,考查计算能力,属于中档题.


 智能训练练测考系列答案
智能训练练测考系列答案科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{1}{2}$,0) | B. | ($\frac{1}{2}$,+∞) | C. | (0,$\frac{1}{2}$) | D. | (-∞,$\frac{1}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
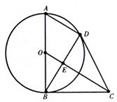 如图所示,AB为圆D的直径,BC为圆O的切线,过A作OC的平行线交圆O于D,BD与OC相交于E.
如图所示,AB为圆D的直径,BC为圆O的切线,过A作OC的平行线交圆O于D,BD与OC相交于E.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 类别 | 有责任 | 无责任 | 总计 |
| 有酒精 | 650 | 150 | 800 |
| 无酒精 | 700 | 500 | 1200 |
| 合计 | 1350 | 650 | 2000 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 男公务员 | 女公务员 | |
| 生二胎 | 80 | 40 |
| 不生二胎 | 40 | 40 |
| P(k2≥k0) | 0.050 | 0.010 | 0.001 |
| K0 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
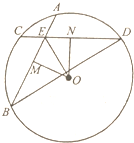 如图,在圆O中,相交于点E的两弦AB,CD的中点分别为M,N.
如图,在圆O中,相交于点E的两弦AB,CD的中点分别为M,N.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com