
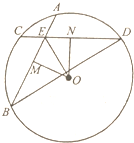
 如图,在圆O中,相交于点E的两弦AB,CD的中点分别为M,N.
如图,在圆O中,相交于点E的两弦AB,CD的中点分别为M,N.分析 (1)由题意可得OM⊥AB,ON⊥CD,可得∠OME+∠ONE=180°,从而得到O,M,E,N四点共圆.
(2)利用条件求得BE=DE,设BD的中点为O1,则EO1⊥BD,OO1⊥BD,证得E,O1,O三点共线,可得EO⊥BD.
解答 解:(1)∵M为AB的中点,∴OM⊥AB;∵N为CD的中点,∴ON⊥CD,
在四边形OMEN中,∴∠OME+∠ONE=180°,∴O,M,E,N四点共圆.
(2)因为AB=CD,所以$\widehat{AB}=\widehat{CD}$,所以$\widehat{BC}=\widehat{AD}$,∴∠ABD=∠BDC,所以BE=DE,
连接OB,OD,设BD的中点为O1,则EO1⊥BD,OO1⊥BD,
所以E,O1,O三点共线,所以EO⊥BD.
点评 本题主要考查与圆有关的比例线段,四点共圆的条件,等腰三角形的性质,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 广播电台为了了解某地区的听众对某个戏曲节目的收听情况,随机抽取了100名听众进行调查,下面是根据调查结果绘制的听众日均收听该节目的频率分布直方图,将日均收听该节目时间不低于40分钟的听众成为“戏迷”
广播电台为了了解某地区的听众对某个戏曲节目的收听情况,随机抽取了100名听众进行调查,下面是根据调查结果绘制的听众日均收听该节目的频率分布直方图,将日均收听该节目时间不低于40分钟的听众成为“戏迷”| “戏迷” | 非戏迷 | 总计 | |
| 男 | |||
| 女 | 10 | 55 | |
| 总计 |
| P(K2≥k) | 0.05 | 0.01 |
| k | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{1}{2}$,$\frac{1}{2}$] | B. | [-$\frac{1}{2}$,0] | C. | [0,$\sqrt{6}$] | D. | [0,$\frac{1}{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
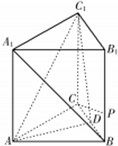 正三棱柱ABC-A1B1C1中,AB=6,AA1=4,D为BC的中点.
正三棱柱ABC-A1B1C1中,AB=6,AA1=4,D为BC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com