
分析 (1)据题意便知集合B至少含3个元素1,2,3,还可由4,5,6,7中的0个、1个、2个、3个,或4个构成集合B的元素,这样根据组合的知识便可求出集合B的个数;
(2)可根据题意看出集合C的元素为1,2,3,4,5,6,7中的相邻的4个数构成的,从而可写出所有符合条件的集合C,进而得出集合C的个数.
解答 解:(1)根据条件知,集合B至少含3个元素1,2,3;
∴集合B的可能情况为:1,2,3和4,5,6,7中的0个、1个、2个、3个、4个元素构成集合B的元素;
∴集合B的个数为${{C}_{4}}^{0}+{{C}_{4}}^{1}+{{C}_{4}}^{2}+{{C}_{4}}^{3}+{{C}_{4}}^{4}={2}^{4}=16$;
(2)根据题意知,集合C的4个元素是1,2,3,4,5,6,7中的4个相邻的数组成的;
∴C的可能情况为{1,2,3,4},{2,3,4,5},{3,4,5,6},{4,5,6,7};
∴集合C的个数是4.
故答案为:16,4.
点评 考查列举法表示集合的定义及表示形式,元素与集合的关系,以及子集的概念,组合的知识,二项式定理.


科目:高中数学 来源: 题型:解答题
| 男公务员 | 女公务员 | |
| 生二胎 | 80 | 40 |
| 不生二胎 | 40 | 40 |
| P(k2≥k0) | 0.050 | 0.010 | 0.001 |
| K0 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
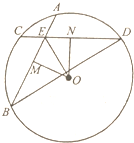 如图,在圆O中,相交于点E的两弦AB,CD的中点分别为M,N.
如图,在圆O中,相交于点E的两弦AB,CD的中点分别为M,N.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | $\sqrt{5}$ | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
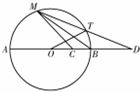 如图所示,直线DA过圆O的圆心,且交圆O于A,B两点,BC=CO=$\frac{1}{2}$BD,DM为圆O的一条割线,且与圆O交于M,T两点.
如图所示,直线DA过圆O的圆心,且交圆O于A,B两点,BC=CO=$\frac{1}{2}$BD,DM为圆O的一条割线,且与圆O交于M,T两点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com