
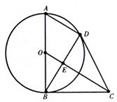
 如图所示,AB为圆D的直径,BC为圆O的切线,过A作OC的平行线交圆O于D,BD与OC相交于E.
如图所示,AB为圆D的直径,BC为圆O的切线,过A作OC的平行线交圆O于D,BD与OC相交于E.分析 (I)连接OD,证明△OBC≌△ODC,可得∠ODC=∠OBC=90°,即可证明CD为圆O的切线;
(Ⅱ)Rt△OBC中,BE⊥OC,OB2=OE•OC,即可求OC的长.
解答 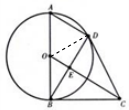 (I)证明:连接OD.
(I)证明:连接OD.
∵AB为圆D的直径,
∴AD⊥DB,
∵AD∥OC,
∴BD⊥OC,
∴E为BD的中点,
∴CB=CD,
∴△OBC≌△ODC,
∴∠ODC=∠OBC=90°,
∴CD为圆O的切线;
(Ⅱ)解:由题意,OB=OA=4,OE=$\frac{1}{2}$AD=2,
Rt△OBC中,BE⊥OC,
∴OB2=OE•OC,
∴OC=$\frac{O{B}^{2}}{OE}$=8.
点评 本题考查圆的切线的证明,考查射影定理,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“?x∈R,均有x2-3x-2≥0”的否定是:“?x∈R,使得x2-3x-2≤0” | |
| B. | “命题p∨q为真命题”是“命题p∧q为真命题”的充分不必要条件 | |
| C. | ?m∈R,使f(x)=mx${\;}^{{m^2}+2m}}$是幂函数,且函数f(x)在(0,+∞)上单调递增 | |
| D. | 若数据x1,x2,x3,…,xn的方差为1,则2x1,2x2,2x3,…,2xn的方差为2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 广播电台为了了解某地区的听众对某个戏曲节目的收听情况,随机抽取了100名听众进行调查,下面是根据调查结果绘制的听众日均收听该节目的频率分布直方图,将日均收听该节目时间不低于40分钟的听众成为“戏迷”
广播电台为了了解某地区的听众对某个戏曲节目的收听情况,随机抽取了100名听众进行调查,下面是根据调查结果绘制的听众日均收听该节目的频率分布直方图,将日均收听该节目时间不低于40分钟的听众成为“戏迷”| “戏迷” | 非戏迷 | 总计 | |
| 男 | |||
| 女 | 10 | 55 | |
| 总计 |
| P(K2≥k) | 0.05 | 0.01 |
| k | 3.841 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com