
分析 (1)去绝对值,再解不等式组可得不等式f(x)<3的解集;
(2)作出f(x)图象,结合图象可得a的取值.
解答 解:(1)去绝对值可得,x<1,-x+1-x+2<3,∴x>0,∴0<x<1;
1≤x≤2,x-1-x+2<3,成立;
x>2,x-1+x-2<3,∴x<3,∴2<x<3,
综上所述,不等式的解集为{x|0<x<3};
(2)f(x)图象如图所示,直线y=a(x+$\frac{1}{2}$)绕点(-$\frac{1}{2}$,0)旋转,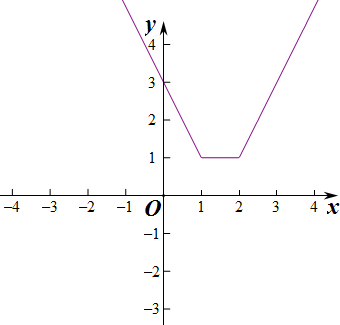
由图可得不等式f(x)≤a(x+$\frac{1}{2}$)的解集非空时,a的范围为(-∞,-2)∪[$\frac{2}{5}$,+∞).
点评 本题考查绝对值不等式的解法及应用,数形结合是解决问题的关键,属中档题.


科目:高中数学 来源: 题型:解答题
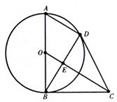 如图所示,AB为圆D的直径,BC为圆O的切线,过A作OC的平行线交圆O于D,BD与OC相交于E.
如图所示,AB为圆D的直径,BC为圆O的切线,过A作OC的平行线交圆O于D,BD与OC相交于E.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 患心肺疾病 | 不患心肺疾病 | 合计 | |
| 男 | m | 6 | |
| 女 | 12 | n | |
| 合计 | 60 |
| P(k2>k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 男公务员 | 女公务员 | |
| 生二胎 | 80 | 40 |
| 不生二胎 | 40 | 40 |
| P(k2≥k0) | 0.050 | 0.010 | 0.001 |
| K0 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | $\sqrt{5}$ | D. | 9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com