
| A�� | ���⡰?x��R������x2-3x-2��0���ķ��ǣ���?x��R��ʹ��x2-3x-2��0�� | |
| B�� | ������p��qΪ�����⡱�ǡ�����p��qΪ�����⡱�ij�ֲ���Ҫ���� | |
| C�� | ?m��R��ʹf��x��=mx${\;}^{{m^2}+2m}}$���ݺ������Һ���f��x���ڣ�0��+�ޣ��ϵ������� | |
| D�� | ������x1��x2��x3������xn�ķ���Ϊ1����2x1��2x2��2x3������2xn�ķ���Ϊ2 |
���� A������ȫ������ķ����س���������жϼ��ɣ�
B�����ݸ���������ٹ�ϵ�Լ���������ͱ�Ҫ�����Ķ�������жϣ�
C�������ݺ����Ķ��������m��Ȼ�����ݺ��������ʽ����жϣ�
D���������ݷ���֮��Ĺ�ϵ�����жϼ��ɣ�
��� �⣺A�����⡰?x��R������x2-3x-2��0���ķ��ǣ���?x��R��ʹ��x2-3x-2��0������A����
B����p��q��ʱ����������p��qΪ�����⣬������p��qΪ�����⣬�����Բ���������B����
C����f��x��=mx${\;}^{{m^2}+2m}}$���ݺ�������m=1����ʱf��x��=x3����ʱ����f��x���ڣ�0��+�ޣ���������������C��ȷ��
D��������x1��x2��x3������xn�ķ���Ϊ1����2x1��2x2��2x3������2xn�ķ���Ϊ4����D����
��ѡ��C
���� ������Ҫ�������������жϣ��漰֪ʶ��϶࣬�ۺ��Խ�ǿ�����ѶȲ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-$\frac{1}{2}$��0�� | B�� | ��$\frac{1}{2}$��+�ޣ� | C�� | ��0��$\frac{1}{2}$�� | D�� | ��-�ޣ�$\frac{1}{2}$�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | [-8��-4+2$\sqrt{5}$�� | B�� | ��-4-2$\sqrt{5}$��-4+2$\sqrt{5}$�� | C�� | ��-4+2$\sqrt{5}$��8] | D�� | ��-4-2$\sqrt{5}$��-8] |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
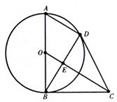 ��ͼ��ʾ��ABΪԲD��ֱ����BCΪԲO�����ߣ���A��OC��ƽ���߽�ԲO��D��BD��OC�ཻ��E��
��ͼ��ʾ��ABΪԲD��ֱ����BCΪԲO�����ߣ���A��OC��ƽ���߽�ԲO��D��BD��OC�ཻ��E���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| �й���Ա | Ů����Ա | |
| ����̥ | 80 | 40 |
| ������̥ | 40 | 40 |
| P��k2��k0�� | 0.050 | 0.010 | 0.001 |
| K0 | 3.841 | 6.635 | 10.828 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com