
分析 (1)求出函数的导数,判断导函数的符号,求出函数的单调区间即可;
(2)问题转化为xemx-1-mx-lnx≥0恒成立且“=”可取,令g(x)=xemx-1-mx-lnx即g(x)min=0,根据函数的单调性求出m的最小值即可.
解答 解:(1)f(x)的定义域是(0,+∞),
m=1时,f(x)=ex-1-$\frac{lnx}{x}$,f′(x)=ex-1-$\frac{1-lnx}{{x}^{2}}$,
x>1时,f′(x)>1-$\frac{1-lnx}{{x}^{2}}$=$\frac{{(x}^{2}-1)+lnx}{{x}^{2}}$>0,
0<x<1时,f′(x)<1-$\frac{1-lnx}{{x}^{2}}$=$\frac{{(x}^{2}-1)+lnx}{{x}^{2}}$<0,
∴f(x)在(0,1]递减,在(1,+∞)递增;
(2)由题意得:emx-1-$\frac{lnx}{x}$≥m时对x>0恒成立且“=”可取,
即xemx-1-mx-lnx≥0恒成立且“=”可取,
令g(x)=xemx-1-mx-lnx即g(x)min=0,
g′(x)=(mx+1)(emx-1-$\frac{1}{x}$),
由emx-1-$\frac{1}{x}$=0得:m=$\frac{1-lnx}{x}$,
设p(x)=$\frac{1-lnx}{x}$,p′(x)=$\frac{lnx-2}{{x}^{2}}$,
x>e2时,p′(x)>0,0<x<e2时,p′(x)<0,
p(x)在(0,e2)递减,在(e2,+∞)递增,
∴p(x)min=p(e2)=-$\frac{1}{{e}^{2}}$,
m≤-$\frac{1}{{e}^{2}}$时,m≤$\frac{1-lnx}{x}$,即emx-1-$\frac{1}{x}$≤0,
在(0,-$\frac{1}{m}$)上,mx+1>0,g′(x)≤0,g(x)递减,
在(-$\frac{1}{m}$,+∞)上,mx+1<0,g′(x)≥0,g(x)递增,
∴g(x)min=g(-$\frac{1}{m}$),令t=-$\frac{1}{m}$∈(0,e2],g(-$\frac{1}{m}$)=h(t)=$\frac{t}{{e}^{2}}$-lnt+1,
h′(t)=$\frac{1}{{e}^{2}}$-$\frac{1}{t}$≤0,h(t)在(0,e2)递减,
∴h(t)≥h(e2)=0,
∴方程g(x)min=g(-$\frac{1}{m}$)=0有唯一解e2=-$\frac{1}{m}$,即m=-$\frac{1}{{e}^{2}}$,
综上,m≤-$\frac{1}{{e}^{2}}$时,仅有m=-$\frac{1}{{e}^{2}}$满足f(x)的最小值为m,
∴m的最小值为-$\frac{1}{{e}^{2}}$.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论,是一道难题.


科目:高中数学 来源: 题型:解答题
| 有震 | 无震 | 总计 | |
| 有变化 | 98 | 902 | 1000 |
| 无变化 | 82 | 618 | 700 |
| 总计 | 180 | 1520 | 1700 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
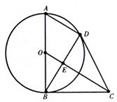 如图所示,AB为圆D的直径,BC为圆O的切线,过A作OC的平行线交圆O于D,BD与OC相交于E.
如图所示,AB为圆D的直径,BC为圆O的切线,过A作OC的平行线交圆O于D,BD与OC相交于E.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 类别 | 有责任 | 无责任 | 总计 |
| 有酒精 | 650 | 150 | 800 |
| 无酒精 | 700 | 500 | 1200 |
| 合计 | 1350 | 650 | 2000 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{5}}}{5}$ | D. | $\frac{{\sqrt{5}-1}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com