
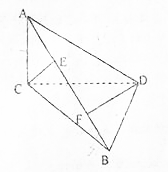
 如图,AC⊥面BCD,BD⊥面ACD,若AC=CD=1,∠ABC=30°,求二面角C-AB-D的大小的余弦值.
如图,AC⊥面BCD,BD⊥面ACD,若AC=CD=1,∠ABC=30°,求二面角C-AB-D的大小的余弦值. 分析 作DF⊥AB于F,CE⊥AB于E,设二面角C-AB-D的大小为θ,则${\overrightarrow{CD}}^{2}={\overrightarrow{CE}}^{2}+{\overrightarrow{EF}}^{2}+{\overrightarrow{FD}}^{2}$-2|$\overrightarrow{CE}$|•$|\overrightarrow{FD}|$•cosθ,由此能求出二面角C-AB-D的余弦值.
解答 解:作DF⊥AB于F,CE⊥AB于E,
∵AC⊥面BCD,BD⊥面ACD,AC=CD=1,∠ABC=30°,
∴AD=$\sqrt{2}$,AB=2,BC=$\sqrt{3}$,BD=$\sqrt{2}$,
在Rt△ABC中,CE=$\frac{AC•BC}{AB}$=$\frac{1×\sqrt{3}}{2}$=$\frac{\sqrt{3}}{2}$,
同理,DF=$\frac{AD•BD}{AB}$=$\frac{\sqrt{2}×\sqrt{2}}{2}$=1,
∴BF=$\sqrt{B{D}^{2}-D{F}^{2}}$=1,AE=$\sqrt{A{C}^{2}-C{E}^{2}}$=$\frac{1}{2}$,
∴EF=2-1-$\frac{1}{2}=\frac{1}{2}$,
设二面角C-AB-D的大小为θ,
∵$\overrightarrow{CD}=\overrightarrow{CE}+\overrightarrow{EF}+\overrightarrow{FD}$,
∴${\overrightarrow{CD}}^{2}={\overrightarrow{CE}}^{2}+{\overrightarrow{EF}}^{2}+{\overrightarrow{FD}}^{2}$-2|$\overrightarrow{CE}$|•$|\overrightarrow{FD}|$•cosθ,
即1=$\frac{3}{4}$+1+$\frac{1}{4}$-2×$\frac{\sqrt{3}}{2}×1×cosθ$,
解得cosθ=$\frac{\sqrt{3}}{3}$.
∴二面角C-AB-D的余弦值为$\frac{\sqrt{3}}{3}$.
点评 本题考查二面角的求法,是中档题,解题时要认真审题,注意向量法的合理运用.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
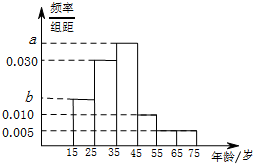 2016年全国两会,即中华人民共和国第十二届全国人民代表大会第四次会议和中国人民政治协商会议第十二届全国委员会第四次会议,分别于2016年3月5日和3月3日在北京开幕.为了解哪些人更关注两会,某机构随抽取了年龄在15~75岁之间的100人进行调查,并按年龄绘制的频率分布直方图如图所示,其分组区间为:[15,25),[25,35),[35,45),[55,65),[65,75].把年龄落在区间[15,35)和[35,75]内的人分别称为“青少年人”和“中老年人”,经统计“青少年人”和“中老年人”的人数之比为9:11.
2016年全国两会,即中华人民共和国第十二届全国人民代表大会第四次会议和中国人民政治协商会议第十二届全国委员会第四次会议,分别于2016年3月5日和3月3日在北京开幕.为了解哪些人更关注两会,某机构随抽取了年龄在15~75岁之间的100人进行调查,并按年龄绘制的频率分布直方图如图所示,其分组区间为:[15,25),[25,35),[35,45),[55,65),[65,75].把年龄落在区间[15,35)和[35,75]内的人分别称为“青少年人”和“中老年人”,经统计“青少年人”和“中老年人”的人数之比为9:11.| 关注 | 不关注 | 合计 | |
| 青少年人 | 15 | ||
| 中老年人 | |||
| 合计 | 50 | 50 | 100 |
| P(K2≥k0) | 0.05 | 0.01 | 0.001 |
| k0 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0) | B. | (0,1] | C. | (0,+∞) | D. | [0,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{1}{2}$,$\frac{1}{2}$] | B. | [-$\frac{1}{2}$,0] | C. | [0,$\sqrt{6}$] | D. | [0,$\frac{1}{2}$] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com