
分析 (I)通过在4Sn=(an+1)2中令n=1可知首项a1=1,当n≥2时利用Sn与an的关系,作差可知an-an-1=2,进而计算可得结论;
(Ⅱ)通过(I)放缩、裂项可知$\frac{1}{{S}_{n}}$<$\frac{1}{n-1}$-$\frac{1}{n}$(n≥2),进而并项相加即得结论.
解答 (I)解:∵4Sn=(an+1)2,
∴令n=1可知,4a1=${{a}_{1}}^{2}$+2a1+1,
∴${{a}_{1}}^{2}$-2a1+1=0,即a1=1,
当n≥2时,4an=(an+1)2-(an-1+1)2,
整理得,(an-an-1)(an+an-1)=2(an+an-1),
又∵数列{an}的各项均为正数,
∴an-an-1=2,a2=1+2=3,
∴数列{an}是首项为1、公差为2的等差数列,
∴an=2n-1;
(Ⅱ)证明:由(I)可知Sn=$\frac{1}{4}$(an+1)2=n2,
∴$\frac{1}{{S}_{n}}$=$\frac{1}{{n}^{2}}$<$\frac{1}{n(n-1)}$=$\frac{1}{n-1}$-$\frac{1}{n}$(n≥2),
∴$\frac{1}{{S}_{1}}$+$\frac{1}{{S}_{2}}$+$\frac{1}{{S}_{3}}$+…+$\frac{1}{{S}_{n}}$<1+1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+…+$\frac{1}{n-1}$-$\frac{1}{n}$<2.
点评 本题考查数列的通项及前n项和,考查裂项相消法,注意解题方法的积累,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 0 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
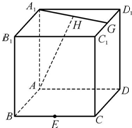 如图,在棱长为1的正方体ABCD-A1B1C1D1中,E是BC的中点,F是棱CD上的动点,G为C1D1的中点,H为A1G的中点.
如图,在棱长为1的正方体ABCD-A1B1C1D1中,E是BC的中点,F是棱CD上的动点,G为C1D1的中点,H为A1G的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知四棱锥S-ABCD的底面ABCD是正方形,SA⊥底面ABCD,E是SC上的一点.
如图,已知四棱锥S-ABCD的底面ABCD是正方形,SA⊥底面ABCD,E是SC上的一点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 成功(人) | 失败(人) | 合计 | |
| 20~30(岁) | 20 | 40 | 60 |
| 30~40(岁) | 50 | ||
| 合计 | 70 |
| P(K2≥k) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
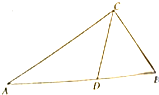
| A. | AC•AD=AB•CD | B. | AC•BC=AB•AD | C. | CD2=AD•DB | D. | AC2=AD•AB |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届甘肃兰州一中高三9月月考数学(理)试卷(解析版) 题型:选择题
已知直线l:x+ay-1=0(a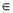 R)是圆C:
R)是圆C: 的对称轴.过点A(-4,a)作圆C的一条切线,切点为B,则|AB|=( )
的对称轴.过点A(-4,a)作圆C的一条切线,切点为B,则|AB|=( )
A.2 B.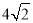 C.6 D.
C.6 D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com