练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    10．已知函数f（x）=$\left\{\begin{array}{l}{2x，（x≤-1）}\\{1，（-1＜x≤1）}\\{-2x，（x＞1）}\end{array}\right.$
    （1）求f（x）的定义域、值域：
    （2）作出这个函数的图象．

    分析 （1）根据分段函数，可得f（x）的定义域、值域：
    （2）根据分段函数作出这个函数的图象．

    解答 解：（1）由题意，f（x）的定义域是R，值域是（-∞，-2]∪{1}；
    （2）作出这个函数的图象，如图所示．

    点评 本题考查分段函数，考查数形结合的数学思想，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    20．若动△ABC内接于抛物线y2=4x，且△ABC的重心恰好是抛物线的焦点，求△ABC面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．己知数列{an}的各项均为正数，其前n项和为Sn，且满足4Sn=（an+1）2．
    （I）求出a1，a2的值，并求数列{an}的通项公式；
    （Ⅱ）求证：$\frac{1}{{S}_{1}}$+$\frac{1}{{S}_{2}}$+$\frac{1}{{S}_{3}}$+…+$\frac{1}{{S}_{n}}$＜2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．如图，平行四边形ABCD中，AE：EB=1：2．
    （ I）求△AEF与△CDF的周长比；
    （ II）如果△AEF的面积等于6cm2，求△CDF的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．设数列{an}的前n项和为Sn，（an，Sn）在函数y=2-x的图象上．
    （1）求an；
    （2）若数列{bn}满足b1=1，bn+1=bn+an，求bn；
    （3）在（2）的条件下，设cn=1og${\;}_{\frac{1}{2}}$a2n，Tn=$\frac{4}{{c}_{1}{c}_{2}}$+$\frac{4}{{c}_{2}{c}_{3}}$+…+$\frac{4}{{c}_{n}{c}_{n+1}}$，若不等式bn+Tn＞m-2013对一切正整数n都成立的，求m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．如图所示，AE、AF分别为△ABC的内、外角平分线，O为EF的中点．
    求证：OB：OC=AB2：AC2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

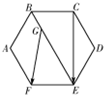    2．已知边长为2的正六边形ABCDEF中，连接BE、CE，点G是线段BE上靠近B的四等分点，连接GF，则$\overrightarrow{GF}$•$\overrightarrow{CE}$=（　　）
    A．-6B．-9C．6D．9

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．设无穷数列{an}的前n项和为Sn，若存在常数k，满足Sn≥k$\sqrt{n}$对一切的n∈N*成立，则称数列{an}为“k数列”
    （1）求证：数列{1-2n}不是“k数列”；
    （2）求证：数列{n-5}是“k数列”，并求出k的最大值．

    查看答案和解析>>

    科目：高中数学 来源：2017届甘肃会宁县一中高三上学期9月月考数学（文）试卷（解析版） 题型：选择题

    设集合M＝{x|－1≤x＜2}，N＝{y|y＜a}，若M∩N≠∅，则实数a的取值范围一定是（ ）

    A.[－1，2） B.（－∞，2] C.[2，＋∞） D.（－1，＋∞）

    查看答案和解析>>

    同步练习册答案