
分析 (1)根据数列的函数特征,求出数列的递推公式,根据递推公式求出数列的通项公式,
(2)利用累加法即可求出数列bn的通项公式,
(3)先根据对数的性质求出数列cn的通项公式,再用裂项求和求出Tn,再分离参数,根据数列的单调性即可求出m的取值范围.
解答 解:(1)数列{an}的前n项和为Sn,(an,Sn)在函数y=2-x的图象上,
∴Sn=2-an,
∴Sn-1=2-an-1,
∴an=an-1-an,
即2an=an-1,
∴$\frac{{a}_{n}}{{a}_{n-1}}$=$\frac{1}{2}$,
当n=1时,S1=2-a1,解的a1=1,
∴数列{an}是以1为首项,以$\frac{1}{2}$为公比的等比数列,
∴an=$\frac{1}{{2}^{n-1}}$,
(2)∵b1=1,bn+1=bn+an,
∴bn-bn-1=an-1,
∴b2-b1=a1,b3-b2=a2,…,
累加可得bn-b1=a1+a2+…+an-1=$\frac{1×(1-\frac{1}{{2}^{n-1}})}{1-\frac{1}{2}}$=2-$\frac{1}{{2}^{n-2}}$,
∴bn=3-$\frac{1}{{2}^{n-2}}$,
(3)∵cn=1og${\;}_{\frac{1}{2}}$a2n=2n-1,
∴$\frac{4}{{c}_{n}{c}_{n+1}}$=$\frac{4}{(2n-1)(2n+1)}$=2($\frac{1}{2n-1}$-$\frac{1}{2n+1}$),
∴Tn=$\frac{4}{{c}_{1}{c}_{2}}$+$\frac{4}{{c}_{2}{c}_{3}}$+…+$\frac{4}{{c}_{n}{c}_{n+1}}$=2($\frac{1}{1}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{5}$+…+$\frac{1}{2n-1}$-$\frac{1}{2n+1}$)=2(1-$\frac{1}{2n+1}$)=2-$\frac{2}{2n+1}$
∵不等式bn+Tn>m-2013对一切正整数n都成立,
∴m<3-$\frac{1}{{2}^{n-2}}$+2-$\frac{2}{2n+1}$+2013=2018-$\frac{1}{{2}^{n-2}}$-$\frac{2}{2n+1}$
设f(n)=2018-$\frac{1}{{2}^{n-2}}$-$\frac{2}{2n+1}$
∴f(n)在n∈N*为递增数列,
∴f(n)min=f(1)=2018-2-$\frac{2}{3}$=2015$\frac{1}{3}$=$\frac{6046}{3}$,
∴m<$\frac{6046}{3}$
点评 本题考查数列的递推关系,考查等差数列的通项公式及数列的裂项法求和,函数恒成立的问题,属于中档题.


 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知四棱锥S-ABCD的底面ABCD是正方形,SA⊥底面ABCD,E是SC上的一点.
如图,已知四棱锥S-ABCD的底面ABCD是正方形,SA⊥底面ABCD,E是SC上的一点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
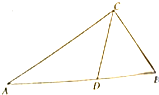
| A. | AC•AD=AB•CD | B. | AC•BC=AB•AD | C. | CD2=AD•DB | D. | AC2=AD•AB |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
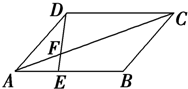
| A. | 16 cm2 | B. | 18 cm2 | C. | 20 cm2 | D. | 22 cm2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届甘肃会宁县一中高三上学期9月月考数学(文)试卷(解析版) 题型:选择题
已知定义在R上的函数f(x)是增函数,且f(1)=1,则使得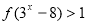 成立的
成立的 的取值范围是( )
的取值范围是( )
A. B.
B. C.
C.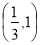 D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com