
 如图,已知四棱锥S-ABCD的底面ABCD是正方形,SA⊥底面ABCD,E是SC上的一点.
如图,已知四棱锥S-ABCD的底面ABCD是正方形,SA⊥底面ABCD,E是SC上的一点.分析 (1)利用SA⊥底面ABCD,可得SA⊥BD.利用ABCD是正方形,可得AC⊥BD,即可证明BD⊥平面SAC,平面EBD⊥平面SAC.
(2)设AC∩BD=O,连接SO,可得SO⊥BD.令点A到平面SBD的距离为h,由SA⊥平面ABCD,利用$\frac{1}{3}$•S△SBD•h=$\frac{1}{3}$•S△ABD•SA,即可得出.
(3 )经过点B作BM⊥SC,垂足为M,连接DM,由对称性可得:DM⊥SC,BM=MD.因此∠BMD是二面角B-SC-D的平面角,又点O为BD的中点,可得OM平分∠BMD,因此只要∠BMO=60°即可,利用S△SBC=$\frac{1}{2}$BM•SC=$\frac{1}{2}$SB•BC,即可解出.
解答 (1)证明:∵SA⊥底面ABCD,BD?底面ABCD,∴SA⊥BD.
∵ABCD是正方形,∴AC⊥BD,
∴BD⊥平面SAC,又BD?平面EBD,
∴平面EBD⊥平面SAC.
(2)解:设AC∩BD=O,连接SO,则SO⊥BD.
由AB=2,知BD=2$\sqrt{2}$,
SO=$\sqrt{SA2+AO2}=\sqrt{42+(\sqrt{2})2}=3\sqrt{2}$,
∴S△SBD=$\frac{1}{2}$ BD•SO=$\frac{1}{2}$•2$\sqrt{2}$•3$\sqrt{2}$=6,
令点A到平面SBD的距离为h,由SA⊥平面ABCD,则$\frac{1}{3}$•S△SBD•h=$\frac{1}{3}$•S△ABD•SA,
∴6h=$\frac{1}{2}$•2•2•4?h=$\frac{4}{3}$∴点A到平面SBD的距离为$\frac{4}{3}$,
(3 )解:经过点B作BM⊥SC,垂足为M,连接DM,由对称性可得:DM⊥SC,BM=MD.
∴∠BMD是二面角B-SC-D的平面角,
又点O为BD的中点,∴OM平分∠BMD,
因此只要∠BMO=60°即可.
设SA=x,
在Rt△BMO中,BM=$\frac{BO}{cos3{0}^{°}}$=$\frac{2\sqrt{6}}{3}$.
又S△SBC=$\frac{1}{2}$BM•SC=$\frac{1}{2}$SB•BC,
∴$\frac{2\sqrt{6}}{3}$$•\sqrt{{x}^{2}+{2}^{2}×2}$=$\sqrt{{x}^{2}+{2}^{2}}$×2,
解得x=2.
∴当SA=2时,二面角B-SC-D的大小为120°.
点评 本题考查了空间位置关系空间角、“等积变形”、勾股定理、等腰三角形的性质,考查了推理能力与计算能力,属于中档题.


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

| P(X2≥k) | 0.100 | 0.050 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
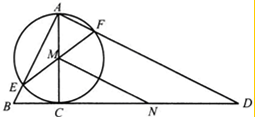 AC是圆O的直径,BD是圆O在点C处的切线,AB、AD分别与圆O相交于E,F,EF与AC相交于M,N是CD中点,AC=4,BC=2,CD=8
AC是圆O的直径,BD是圆O在点C处的切线,AB、AD分别与圆O相交于E,F,EF与AC相交于M,N是CD中点,AC=4,BC=2,CD=8查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 喜欢 | 不喜欢 | 总计 | |
| 男生 | 20 | ||
| 女生 | 20 | ||
| 总计 | 30 | 55 |
| P(K2≥k0) | 0.025 | 0.01 | 0.005 | 0.001 |
| k0 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com