
分析 过点B作BM⊥AA1于M,连结CM,在△ABM和△ACM中,证明ABM≌△ACM,推出AA1⊥面BMC,求出BMC周长,求解S侧.然后求解全面积.
解答 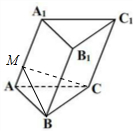 解:过点B作BM⊥AA1于M,连结CM,在△ABM和△ACM中,
解:过点B作BM⊥AA1于M,连结CM,在△ABM和△ACM中,
∵AB=AC,∠MAB=∠MAC=60°,MA为公用边,
∴△ABM≌△ACM,∴∠AMC=∠AMB=90°,∴AA1⊥面BMC,
即平面BMC为直截面,
又BM=CM=ABsin60°=$\frac{\sqrt{3}}{2}$a,
∴BMC周长为2x$\frac{\sqrt{3}}{2}a$+a=(1+$\sqrt{3}$)a,且棱长为$\frac{3}{2}$a,
∴S侧=(1+$\sqrt{3}$)a•$\frac{3}{2}$a.2S底=$\frac{\sqrt{3}}{2}{a}^{2}$.
全面积为:$\frac{3+4\sqrt{3}}{2}{a}^{2}$.
故答案为:$\frac{3+4\sqrt{3}}{2}{a}^{2}$.
点评 本题考查棱柱的结构特征,全面积的求法,考查空间想象能力以及计算能力.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,弦AB与CD相交于圆O内一点E,过E作BC的平行线与AD的延长线交于点P,且PD=2DA.
如图,弦AB与CD相交于圆O内一点E,过E作BC的平行线与AD的延长线交于点P,且PD=2DA.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知四棱锥S-ABCD的底面ABCD是正方形,SA⊥底面ABCD,E是SC上的一点.
如图,已知四棱锥S-ABCD的底面ABCD是正方形,SA⊥底面ABCD,E是SC上的一点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年龄 | [5,15) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 支持“生育二胎” | 4 | 5 | 12 | 8 | 2 | 1 |
| 年龄不低于45岁的人 | 年龄低于45岁的人 | 合计 | |
| 支持“生育二胎” | a=3 | c=29 | 32 |
| 不支持“生育二胎” | b=7 | d=11 | 18 |
| 合计 | 10 | 40 | n=50 |
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 16 cm2 | B. | 18 cm2 | C. | 20 cm2 | D. | 22 cm2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com