
���� ����������Բ���̣����a��c����������ԲC�������ʣ�
������$\frac{{{x_0}x}}{2}+{y_0}y=1$�����A�����꣬Ȼ�����B�����꣬��ʾ�����ε������ͨ��P��x0��y0������ԲC�ϣ����û�������ʽ���������OAB�������Сֵ��
������$\frac{x^2}{{2{��^2}}}$+$\frac{y^2}{��^2}$=1�����$-\sqrt{2}�ˣ�{x_0}��\sqrt{2}��$���ٵ�x0=0ʱ�����P��0���ˣ���Q��-�ˣ�2�ˣ���֤������Q��P��F2���ߣ��ڵ�x0��0ʱ����Q��m��n����m��-�ˣ�F1Q���е�ΪM����$M��\frac{m-��}{2}��\frac{n}{2}��$������ֱ��l�ķ��̣����Q���꣬ͨ����P�ĺ��������F2�ĺ��������ʱ��˵��P��Q��F2���㹲�ߣ���P�ĺ��������F2�ĺ����겻���ʱ��֤��${k_{{F_2}Q}}={k_{{F_2}P}}$��˵��Q��P��F2���㹲�ߣ�
��� ����С������14�֣�
�⣺��������$a=\sqrt{2}��$��$c=\sqrt{2{��^2}-{��^2}}=��$��
������ԲC������Ϊ$e=\frac{��}{{\sqrt{2}��}}=\frac{{\sqrt{2}}}{2}$������3�֣�
����������x0��0����y=0����$\frac{{{x_0}x}}{2}+{y_0}y=1$����$x=\frac{2}{x_0}$����$A��\frac{2}{x_0}��0��$��
��x=0����$\frac{{{x_0}x}}{2}+{y_0}y=1$����$y=\frac{1}{y_0}$����$B��0��\frac{1}{y_0}��$��
���OAB�����${S_{��OAB}}=\frac{1}{2}|{OA}||{OB}|=\frac{1}{2}|{\frac{2}{{{x_0}{y_0}}}}|=\frac{1}{{|{{x_0}{y_0}}|}}$��
��ΪP��x0��y0������ԲC��$\frac{x^2}{2}+{y^2}=1$�ϣ�����$\frac{{{x_0}^2}}{2}+{y_0}^2=1$��
����$1=\frac{{{x_0}^2}}{2}+{y_0}^2��2\frac{{|{{x_0}{y_0}}|}}{{\sqrt{2}}}$����$|{{x_0}{y_0}}|��\frac{{\sqrt{2}}}{2}$����$\frac{1}{{|{{x_0}{y_0}}|}}��\sqrt{2}$��
����${S_{��OAB}}=\frac{1}{2}|{OA}||{OB}|=\frac{1}{{|{{x_0}{y_0}}|}}��\sqrt{2}$��
���ҽ���$\frac{{{x_0}^2}}{2}={y_0}^2$����${x_0}=��1��{y_0}=��\frac{{\sqrt{2}}}{2}$ʱ����OAB�������СֵΪ$\sqrt{2}$�� ����8�֣�
������$\frac{y_0^2}{��^2}=1-\frac{x_0^2}{{2{��^2}}}��0$�����$-\sqrt{2}�ˣ�{x_0}��\sqrt{2}��$��
�ٵ�x0=0ʱ��P��0���ˣ���Q��-�ˣ�2�ˣ�����ʱ${k_{{F_2}P}}=-1$��${k_{{F_2}Q}}=-1$��
��Ϊ${k_{{F_2}Q}}={k_{{F_2}P}}$����������Q��P��F2���ߣ�
��P��0��-�ˣ�ʱ��Ҳ���㣮
�ڵ�x0��0ʱ����Q��m��n����m��-�ˣ�F1Q���е�ΪM����$M��\frac{m-��}{2}��\frac{n}{2}��$������ֱ��l�ķ��̣��ã�${x_0}m+2{y_0}n-{x_0}��-4{��^2}=0$��
��ֱ��F1Q��б��Ϊk����$k=\frac{n}{m+��}=\frac{{2{y_0}}}{x_0}$��
����2y0m-x0n+2y0��=0����$\left\{{\begin{array}{l}{{x_0}m+2{y_0}n-{x_0}��-4{��^2}=0}\\{2{y_0}m-{x_0}n+2{y_0}��=0}\end{array}}\right.$��
���$m=\frac{{2x_0^2��+4{x_0}{��^2}}}{4y_0^2+x_0^2}-��$��$n=\frac{{4{x_0}{y_0}��+8{y_0}{��^2}}}{4y_0^2+x_0^2}$��
����$Q��\frac{{2x_0^2��+4{x_0}{��^2}}}{4y_0^2+x_0^2}-�ˣ�\frac{{4{x_0}{y_0}��+8{y_0}{��^2}}}{4y_0^2+x_0^2}��$��
����P�ĺ��������F2�ĺ��������ʱ����x0=�ˣ�$y_0^2=\frac{��^2}{2}$����$m=\frac{{2x_0^2��+4{x_0}{��^2}}}{4y_0^2+x_0^2}-��$����m=�ˣ�
��P��Q��F2���㹲�ߣ�
����P�ĺ��������F2�ĺ����겻���ʱ��
ֱ��F2P��б��Ϊ${k_{{F_2}P}}=\frac{y_0}{{{x_0}-��}}$��
��$-\sqrt{2}�ˡ�{x_0}��\sqrt{2}��$��x0��-2�ˣ�
����ֱ��F2Q��б��Ϊ${k_{{F_2}Q}}=\frac{{\frac{{4{x_0}{y_0}��+8{y_0}{��^2}}}{4y_0^2+x_0^2}}}{{\frac{{2{x_0}^2��+4{x_0}{��^2}}}{4y_0^2+x_0^2}-2��}}=\frac{{4{x_0}{y_0}��+8{y_0}{��^2}}}{{2{x_0}^2��+4{x_0}{��^2}-8y_0^2��-2x_0^2��}}$
=$\frac{{4{x_0}{y_0}��+8{y_0}{��^2}}}{{4{x_0}{��^2}-8y_0^2��}}=\frac{{{x_0}{y_0}+2{y_0}��}}{{{x_0}��-2y_0^2}}=\frac{{{y_0}��{x_0}+2�ˣ�}}{{{x_0}^2+��{x_0}-2{��^2}}}$
=$\frac{{{y_0}��{x_0}+2�ˣ�}}{{��{x_0}-�ˣ���{x_0}+2�ˣ�}}=\frac{y_0}{{{x_0}-��}}$��
��Ϊ${k_{{F_2}Q}}={k_{{F_2}P}}$������Q��P��F2���㹲�ߣ�
��������Q��P��F2���㹲�ߣ�����14�֣�
���� ���⿼��ֱ������Բ���ۺ�Ӧ�ã���Բ�ļ����ʵ�Ӧ�ã�����ת��˼���Լ���������˼���Ӧ�ã��������������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

| P��X2��k�� | 0.100 | 0.050 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 6.635 | 10.828 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
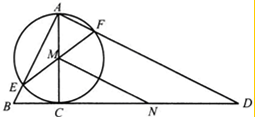 AC��ԲO��ֱ����BD��ԲO�ڵ�C�������ߣ�AB��AD�ֱ���ԲO�ཻ��E��F��EF��AC�ཻ��M��N��CD�е㣬AC=4��BC=2��CD=8
AC��ԲO��ֱ����BD��ԲO�ڵ�C�������ߣ�AB��AD�ֱ���ԲO�ཻ��E��F��EF��AC�ཻ��M��N��CD�е㣬AC=4��BC=2��CD=8�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ϲ�� | ��ϲ�� | �ܼ� | |
| ���� | 20 | ||
| �� | 20 | ||
| �ܼ� | 30 | 55 |
| P��K2��k0�� | 0.025 | 0.01 | 0.005 | 0.001 |
| k0 | 5.024 | 6.635 | 7.879 | 10.828 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��Բ$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1��a��b��0���ľ������ĵ��ҳ�Ϊ��Բ��һ��ֱ����ƽ���ڸ�ֱ���������ҵ��е�Ĺ켣Ϊһ���߶Σ���Ϊ��ֱ���Ĺ���ֱ������֪��Բ�ķ���Ϊ$\frac{x^2}{4}$+y2=1��
��Բ$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1��a��b��0���ľ������ĵ��ҳ�Ϊ��Բ��һ��ֱ����ƽ���ڸ�ֱ���������ҵ��е�Ĺ켣Ϊһ���߶Σ���Ϊ��ֱ���Ĺ���ֱ������֪��Բ�ķ���Ϊ$\frac{x^2}{4}$+y2=1���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com