
分析 (Ⅰ)求出导函数,根据导函数的概念求解即可;
(Ⅱ)构造函数$h(x)=x+\frac{1}{x}-mf(x)=x+\frac{1}{x}-mlnx+\frac{m}{x}$,只需求出函数的最小值小于零即可,求出函数的导函数,对参数m进行分类讨论,判断函数的单调性,求出函数的最小值,最后得出m 的范围..
解答 解:(Ⅰ)∵$f'(x)=\frac{1}{x}-\frac{a}{x^2}$,函数f(x)在x=1处的切线平行于直线2x-y=0.
∴f'(1)=1-a=2
∴a=-1
(Ⅱ)若在[1,e](e=2.718…)上存在一点x0,使得${x_0}+\frac{1}{x_0}<mf({x_0})$成立,
构造函数$h(x)=x+\frac{1}{x}-mf(x)=x+\frac{1}{x}-mlnx+\frac{m}{x}$的最小值小于零.
$h'(x)=1-\frac{1}{x^2}-\frac{m}{x}-\frac{m}{x^2}=\frac{{{x^2}-mx-m-1}}{x^2}=\frac{(x+1)(x-m-1)}{x^2}$…(6分)
①当m+1≥e时,即m≥e-1时,h'(x)<0,h(x)单调递减,…(8分)
由$h(e)=e+\frac{1+m}{e}-m<0$可得$m>\frac{{{e^2}+1}}{e-1}$,
因为$\frac{{{e^2}+1}}{e-1}>e-1$,所以$m>\frac{{{e^2}+1}}{e-1}$; …(10分)
②当m+1≤1,即m≤0时,h'(x)>0,h(x)单调递增,
由h(1)=1+1+m<0可得m<-2; …(11分)
③当1<m+1<e,即0<m<e-1时,
最小值为h(1+m),
因为0<ln(1+m)<1,所以,0<mln(1+m)<m,
h(1+m)=2+m-mln(1+m)>2
此时,h(1+m)<0不成立.
综上所述:可得所求m的范围是:$m>\frac{{{e^2}+1}}{e-1}$或m<-2.…(12分)
点评 考查了导数的概念和存在问题的转化,利用导函数求函数的最值问题.


 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案科目:高中数学 来源: 题型:选择题
| A. | {x|-1≤x≤2} | B. | {x|1<x≤2} | C. | {x|1≤x≤2} | D. | ∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,矩形ABEF所在的平面与等边△ABC所在的平面垂直,AB=2,AF=1,O为AB的中点.
如图,矩形ABEF所在的平面与等边△ABC所在的平面垂直,AB=2,AF=1,O为AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
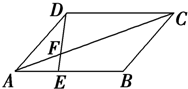
| A. | 16 cm2 | B. | 18 cm2 | C. | 20 cm2 | D. | 22 cm2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com