
| 喜欢 | 不喜欢 | 总计 | |
| 男生 | 20 | ||
| 女生 | 20 | ||
| 总计 | 30 | 55 |
| P(K2≥k0) | 0.025 | 0.01 | 0.005 | 0.001 |
| k0 | 5.024 | 6.635 | 7.879 | 10.828 |
分析 (1)根据表中以有的数据,完成2×2列联表;
(2)根据2×2列联表,代入求临界值的公式,求出观测值,利用观测值同临界值表进行比较,K2≈11.978>10.828,在犯错误的概率不超过0.005的前提下认为喜欢“统计”课程与性别有关.
解答 解:(1)完成2×2列联表:
| 喜欢 | 不喜欢 | 总计 | |
| 男生 | 20 | 5 | 25 |
| 女生 | 10 | 20 | 30 |
| 总计 | 30 | 25 | 55 |
点评 本题考查独立性检验知识的运用,考查计算能力,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知四棱锥S-ABCD的底面ABCD是正方形,SA⊥底面ABCD,E是SC上的一点.
如图,已知四棱锥S-ABCD的底面ABCD是正方形,SA⊥底面ABCD,E是SC上的一点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年龄 | [5,15) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 支持“生育二胎” | 4 | 5 | 12 | 8 | 2 | 1 |
| 年龄不低于45岁的人 | 年龄低于45岁的人 | 合计 | |
| 支持“生育二胎” | a=3 | c=29 | 32 |
| 不支持“生育二胎” | b=7 | d=11 | 18 |
| 合计 | 10 | 40 | n=50 |
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
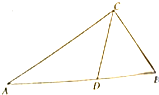
| A. | AC•AD=AB•CD | B. | AC•BC=AB•AD | C. | CD2=AD•DB | D. | AC2=AD•AB |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
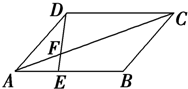
| A. | 16 cm2 | B. | 18 cm2 | C. | 20 cm2 | D. | 22 cm2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届甘肃会宁县一中高三上学期9月月考数学(文)试卷(解析版) 题型:解答题
选修4—5:不等式选讲
已知函数f(x)=|2x-a|+a.
(1)若不等式f(x)≤6的解集为{x|-2≤x≤3},求实数a的值;
(2)在(1)的条件下,若存在实数n使f(n)≤m-f(-n)成立,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com