
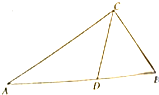
| A. | AC•AD=AB•CD | B. | AC•BC=AB•AD | C. | CD2=AD•DB | D. | AC2=AD•AB |
科目:高中数学 来源: 题型:解答题
| 常喝 | 不常喝 | 合计 | |
| 肥胖 | 6 | 2 | 8 |
| 不肥胖 | 4 | 18 | 22 |
| 合计 | 10 | 20 | 30 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
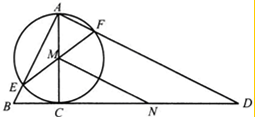 AC是圆O的直径,BD是圆O在点C处的切线,AB、AD分别与圆O相交于E,F,EF与AC相交于M,N是CD中点,AC=4,BC=2,CD=8
AC是圆O的直径,BD是圆O在点C处的切线,AB、AD分别与圆O相交于E,F,EF与AC相交于M,N是CD中点,AC=4,BC=2,CD=8查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 喜欢 | 不喜欢 | 总计 | |
| 男生 | 20 | ||
| 女生 | 20 | ||
| 总计 | 30 | 55 |
| P(K2≥k0) | 0.025 | 0.01 | 0.005 | 0.001 |
| k0 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,平行四边形ABCD中,AE:EB=1:2.
如图,平行四边形ABCD中,AE:EB=1:2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
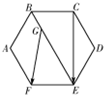 已知边长为2的正六边形ABCDEF中,连接BE、CE,点G是线段BE上靠近B的四等分点,连接GF,则$\overrightarrow{GF}$•$\overrightarrow{CE}$=( )
已知边长为2的正六边形ABCDEF中,连接BE、CE,点G是线段BE上靠近B的四等分点,连接GF,则$\overrightarrow{GF}$•$\overrightarrow{CE}$=( )| A. | -6 | B. | -9 | C. | 6 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源:2017届甘肃会宁县一中高三上学期9月月考数学(文)试卷(解析版) 题型:解答题
已知函数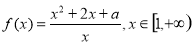 .
.
(1)当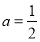 时,求函数
时,求函数 的最小值;
的最小值;
(2)若对任意x∈[1,+∞),f(x)>0恒成立,试求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com